Расчет шпунта и шпунтовых ограждений
Возведение шпунтового ограждения начинается с проектирования, на этом этапе производится оценка условий строительной площадки и возможность геотехнических рисков, составляется проект на проведение работ. На основе этого проекта выполняются многочисленные математические и аналитические расчеты шпунтов.
Поскольку установка шпунтового ограждения является достаточно серьезным строительным процессом, любые нарушения которого могут обернуться неприятными последствиями, то расчет должны производить профессиональные специалисты или компании, имеющие лицензии на такие работы. Следовательно в конце мы порекомендуем обратиться к таким специалистам.
Расчет шпунтового ограждения
Во время расчета шпунтового ограждения, определяются:
- параметры требуемого сечения шпунта,
- глубина его забивки
- необходимость принятия дополнительных мер по укреплению.
В ходе сооружения шпунтового ограждения нагрузка давления грунта на шпунт одинакова с обеих сторон.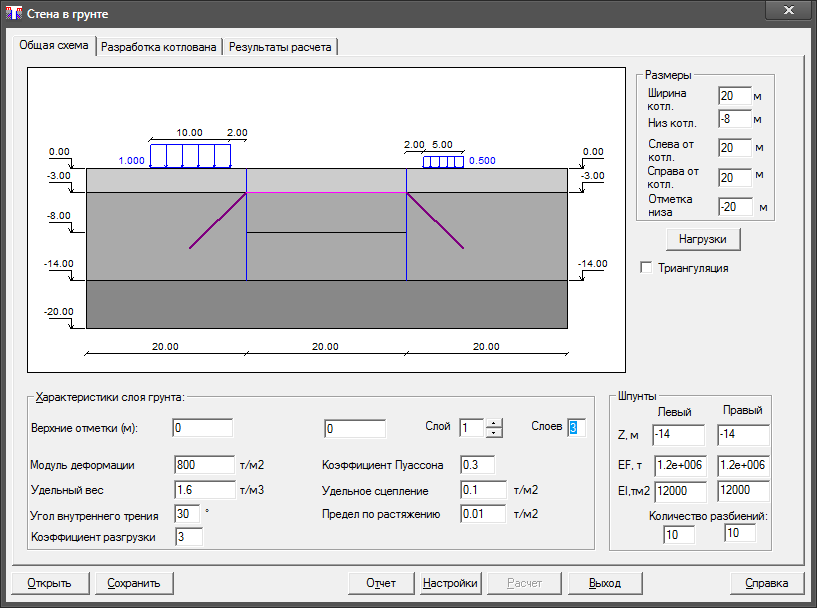
Полезный для Вас материал:
Методики расчета шпунтовых стенок
Для расчета шпунтов пользуются графоаналитическим методом упругой линии, известным также как метод Блюма — Ломейера, или формулой, в которой учтены такие параметры, как глубина котлована, размер вертикальных нагрузок от сооружения, предусмотренный проектом и показатели давления (активного и пассивного) грунта и воды.
При расчете необходимо обратить внимание на вид шпунтовых стенок, которые могут быть безанкерными или анкерными.
Это важный момент, потому что в первом случае точка оборота шпунта находится на дне котлована, а во втором – в месте установки анкерной растяжки.
Для расчета шпунтов берут за основу такие параметры глубины погружения:
- для водозащитной подушки – от 1 м для любого грунта,
- для плотных грунтов – от 1 м,
- для глинистого, песчаного, илистого и суглинистого грунта – от 2 м.
Согласно стандарту СТП 136-99 расчет шпунтовых ограждений определяет параметры устойчивости положения и прочности материала их элементов на различных стадиях разработки котлована, параметры устойчивости днища котлована против выпучивания, минимальная глубина забивки шпунта, расчетное сопротивление элементов и другие показатели.
Формулы расчета по шпунтам
Для расчета устойчивости стены на опрокидывание
,
в которой Mz и Mu — соответствующие расчетные моменты удерживающих и опрокидывающихся нагрузок, m – коэффициент для вязких грунтов, Yn — коэффициент надежности.
Расчет прочности шпунтовой стены
,
где Мр – расчетный момент в сечении шпунтовой стены, Wcm – момент сопротивления шпунтовой стенки (берется из справочников для данного типа шпунта), Rу – расчетные параметры сопротивления материала обвязки, m – коэффициент условий работы.
Частые вопросы
— какая допустимая высота шпунта остаётся над поверхностью земли для возможности его перестановки на следующую захватку ?— Это зависит от модели вибропогружателя,в среднем 30-40см.
— Какова оборачиваемость шпунта Ларсена при забивке в суглинистых и песчанных грунтах ?— Если есть опыт, то импортный шпунт до 20 раз,отечественный до 13раз.
Материалы для Вас:
Использование компьютерных программ для расчёта
Для расчета шпунтового ограждения можно применять различные программные продукты, в частности большое распространение получила программа СпИн, имеющая дружественный пользовательский интерфейс. С ее помощью можно получить данные о ширине или диаметре шпунта из труб, шаге установки и необходимой глубине забивки, а также информацию о рекомендуемом типе стены (анкерная или безанкерная). На скриншоте продемонстрированы примеры окна программы для детального расчета шпунтовых ограждений.
Рассчитать шпунт Ларсена можно и в СКАДe, а также с помощью программного комплекса «ЛИРА».
Мы занимаемся фундаментными работами
Специалисты нашей компании выполнят расчёт, поставку и погружение шпунтовых свай на Ваши объекты. Мы работаем с разными видами фундаментов, имеем богатый опыт.Наша компания занимается фундаментными работами в Москве и регионе — обращайтесь, поможем!
Расчет шпунтового ограждения котлована
Современные геотехнические методы расчета шпунтового ограждения котлована можно разделить на две группы:
- Аналитические расчеты,
- Расчеты методом конечных элементов с использованием программных комплексов — Plaxis расчеты.
Аналитический расчет шпунтового ограждения
Расчет шпунтового ограждения котлована аналитическими методами, выполняется по двум наиболее известным подходам:
Расчет по схеме Якоби.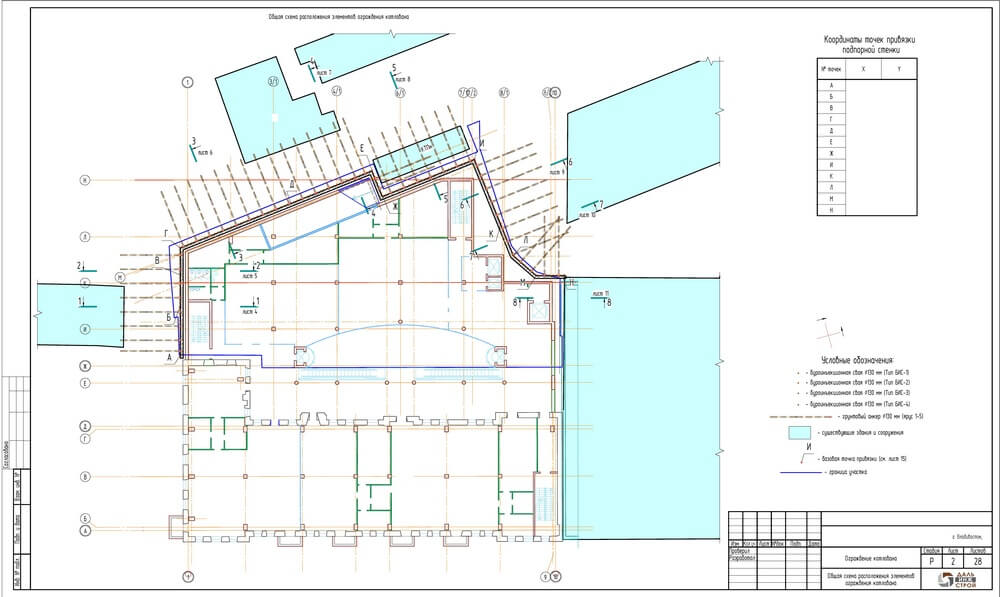
В этом случае глубина погружения стенки определяется только условием обеспечения ее статического равновесия против выпора.
Метод упругой линии (Блюма-Ломейера)
При использовании графоаналитического метода Блюма-Ломейера, глубина погружения определяется из условия получения минимальных значений изгибающих моментов в стенке.
Рисунок 1. Различие подходов аналитического расчета ограждения котлована
В основе аналитических расчетов заложена теория предельного равновесия, основанная Шарлем Кулоном в 1773 году.
На практике, перечисленные методы позволяют определить требуемую длину ограждающей конструкции исходя из условия ее предельного равновесия.
В качестве исходных данных для расчета шпунтового ограждения требуются параметры: удельный вес грунта, удельное сцепление, угол внутреннего трения. Перечисленные параметры могут быть определены достаточно быстро, полевыми методами, в лаборатории или же приняты по справочным данным.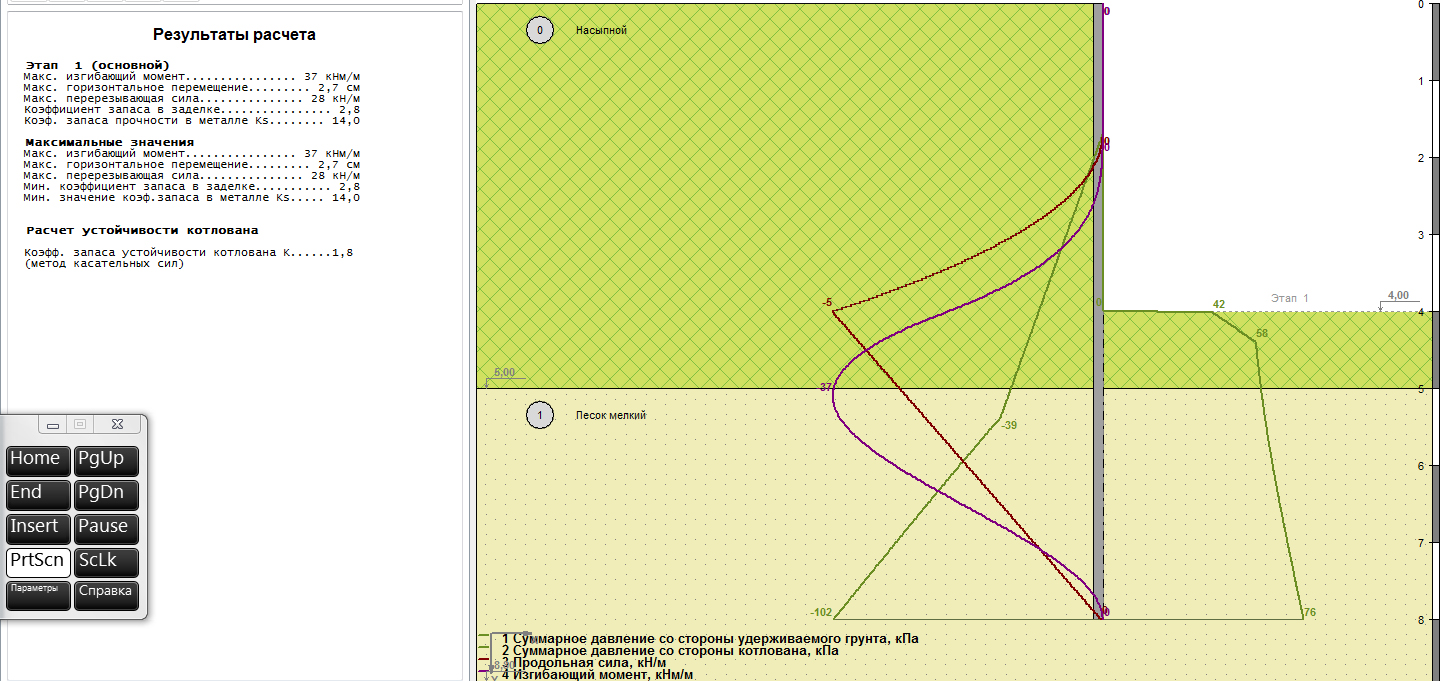
Аналитические методы расчета шпунта, при своей простоте, обладают целым рядом недостатков, связанных прежде всего с ограничениями и допущениями, заложенными в теории расчета:
- предполагается, что плоскости скольжения являются плоскими, когда на самом деле они криволинейные,
- значение давления на ограждающую конструкцию не зависит от направления и величины ее перемещения, когда на практике давление может принимать значения от активного до пассивного,
- призма обрушения ведет себя как твердое тело, что делает возможным использование теории равновесия,
- при выполнении расчетов не учитывается жесткость ограждающей конструкции, определение изгибающих моментов и требуемой жесткости ограждения выполняется постфактум.
Аналитические методы, при всех своих преимуществах не позволяют определить реальные перемещения ограждающей конструкции, а также выполнить геотехнический прогноз влияния строительства на окружающую застройку.
На сегодняшний день существует множество программ, которые позволяют выполнить расчет шпунтового ограждения котлована без трудоемких графических построений и громоздких формул.
Выполняя геотехнические расчеты аналитическими методами, всегда необходимо помнить об ограничениях данных методов, относиться к полученным результатам с недоверием и всегда проверять полученные результаты альтернативными методами, прежде чем использовать их в проекте шпунтового ограждения.
Расчеты методом конечных (FEM – final element method)
Геотехнические расчеты методом конечных элементов выполняются с использованием специализированных программных комплексов, специально разработанных для анализа деформаций и устойчивости геотехнических сооружений. Программы позволяет поэтапно моделировать процессы строительства и экскавации грунта, приложения нагрузок, изменения уровня грунтовых вод, решать задачи консолидации и оценки влияния нового строительства на окружающую завтройку.
Рисунок 2. Сравнение плоской и пространственной постановки задачи в программном комплексе Plaxis
Сравнение плоской и пространственной постановки задачи в программном комплексе Plaxis
Наибольшую популярность среди программных комплексов расчета шпунтового ограждения получили программы Plaxis и Midas GTS NX.
Среди других геотехнических программных комплексов, получивших определенное признание и популярность в мире, следует выделить:
Программы поставляются в различных вариантах, к примеру компания Plaxis BV выпускает программы отдельно для плоских расчетов – Plaxis 2D и отдельно для пространственных расчетов – Plaxis 3D. Компания Midas выпускает программу GTS NX с базовой функцией выполнения как плоских, так и пространственных расчетов.
Стоимость перечисленных программ является довольно высокой. Комплекс для решения задач в плоской постановке может стоить порядка 15000 евро, комплекс для расчета задач в пространственной постановке может обойтись вам в 25000 евро и более.
Специализированные комплексы позволяют выполнять следующие геотехнические расчеты:
- расчеты устойчивости склонов и насыпей,
- расчет конструкций инженерной защиты, методов крепления склонов нагелями, подпорными стенками, габионами и другие,
- расчет фильтрации грунтовых вод,
- расчет консолидации грунтов,
- расчеты оснований и фундаментов, расчет осадки здания,
- расчет шпунтового ограждения и временных конструкций его крепления, при проектировании котлованов,
- расчет тоннелей,
- динамические расчеты, расчеты на сейсмическое воздействие,
- оценка влияния нового строительства на окружающую застройку – это одно из главных преимуществ использования современных программ.
 Специализацией нашей компании является геотехническое обоснование строительства,
Специализацией нашей компании является геотехническое обоснование строительства, - определение зоны влияния нового строительства
Поскольку каждая из программ имеет свои преимущества и недостатки, мы выполняем геотехнические расчеты с использованием трех программных комплексов, в зависимости от сложности поставленной задачи. За более чем 8 летний стаж мы хорошо знаем какой метод позволит получить наиболее реалистичный результат и определить наиболее экономичное конструктивное решение выполняя проект котлована.
В большинстве случаев достаточно выполнить расчет в плоской постановке, однако, если выполняется проектирование котлована сложной формы, пример которого показан на рисунке ниже, геотехнический расчет шпунтового ограждения в плоской постановке может дать чрезмерный запас. Связано это с тем, что любые углы — это элементы большой жесткости, а учет пространственной жесткости может дать значительный экономический эффект, что необходимо учитывать выполняя проект ограждения котлована.
Рисунок 3. Пример котлована сложной формы
Необходимо отметить важную роль, которую играет инженер-геотехник, при выполнении геотехнических расчетов как аналитическими методами, так и с использованием современных программных комплексов. В условиях отсутствия специализированного образования, хороший геотехник это большая редкость. Для воспитания хорошего специалиста могут потребоваться года. К области знаний инженера-геотехника предъявляются особые требования, в которые должны входить:
- Глубокое понимание методов геотехнических расчетов, их преимуществ и ограничений,
- Инженерные знания. Понимание принципов работы строительных конструкции, основы курсов сопротивления материалов, строительной механики и других базовых навыков инженера-строителя,
- Знания в области инженерно-геологических изысканий, полевых и лабораторных методов получения параметров грунтов. Обработка данных с целью получения необходимых параметров для использования в современных комплексах.
 Проверка адекватности параметров, полученных геологами.
Проверка адекватности параметров, полученных геологами. - Знания в области организации строительства и технологий выполнения работ, существующих методов устройства свай, ограждающих конструкций, методов откопки котлована. Необходимо знать пределы применимости той или иной технологии.
- Опыт моделирования в программных комплексах. Как известно, одну и ту же конструкцию можно смоделировать разным образом. Задача геотехника наиболее точно отразить поведение конструкции, здания и других элементов расчетной схемы. Это невозможно сделать, если постоянно не совершенствовать навыки, не сомневаться и не проверять расчеты другим, альтернативными методами. В связи с этим, нами отводится особая роль исследованиям, выступлениям на международных конференциях, накоплению знаний и преемственности.
- Опыт практической реализации проектов. Только он позволяет понять с какими трудностями приходится сталкиваться строителям на площадке. Опыт позволяет принимать решения, которые будут одновременно надежными и простыми в исполнении.
 Позволяет сопоставить результаты геотехнических расчетов с реальностью выполнения проекта шпунтового ограждения котлована в жизнь.
Позволяет сопоставить результаты геотехнических расчетов с реальностью выполнения проекта шпунтового ограждения котлована в жизнь.
Инженер-геотехник объединяет в себе области знаний инженера-строителя и инженера-геолога. Он является их соединительным звеном и неотъемлемой частью процесса проектирования.
Мы специализируемся на выполнении расчетов и проектировании котлованов любой сложности. Позвоните нам, чтобы получить бесплатную консультацию.
Расчет шпунтовых ограждений котлованов, расположенных ниже уровня воды
Шпунтовое ограждение котлованов рассчитывают, чтобы определить необходимую глубину забивки шпунта ниже уровня дна котлована, а также для того, чтобы определить сечение шпунтовых свай и дополнительных креплений (распорок, обвязок). Расчет на прочность и устойчивость проектируемого шпунтового ограждения следует выполнять на стадии полного удаления воды и грунта со дна котлована, в процессе разработки распорных креплений для шпунтового ограждения котлована, а также во время обратной засыпки грунта в котлован и снятия этих креплений.
Мы постараемся рассмотреть случаи расчета шпунтовых ограждений котлованов, которые расположены на горизонтальном грунте в отсутствии над шпунтовым ограждением дополнительных нагрузок в виде стройматериалов, транспортных средств или оборудования.
В тех шпунтовых ограждениях, которые заглублены в супеси или пески, кроме обычного расчета, также в обязательном порядке нужно проверять глубину забивки шпунтовых свай ниже уровня дна котлована или же отметки размыва, чтобы исключить наплыв грунта в котлован во время откачки из него воды.
Независимо от того, каким будет результат расчета, глубина забивки шпунта ниже уровня котлована должна быть, в случае текучих глин, а также водонасыщенных илов и прочих мягких грунтов, не меньше, чем 2 метра, в остальных же случаях ограничение уменьшается до 1 метра (кроме скальных грунтов). Минимальная глубина забивки шпунта определяется, чтобы исключить опасность наплыва грунта во время откачки воды.
Расчетные давления грунта и воды получаются из умножения известных нормативных давлений на коэффициент надежности по нагрузке (или перегрузке). При этом, коэффициент перегрузки принимает значение 1,2 для активного давления грунта и 0,8 – для пассивного.
При этом, коэффициент перегрузки принимает значение 1,2 для активного давления грунта и 0,8 – для пассивного.
Влияние фильтрационного потока во время откачки воды из котлована в расчетах не учитывается.
При строительстве шпунтового ограждения в водопроницаемых грунтах с подводной водозащитной подушкой в расчете также нужно учитывать дополнительные параметры. Например, при расчете шпунтового ограждения в тот момент, когда водозащитная подушка еще не будет забетонирована, нужно учесть еще и гидростатическое давление, которое будет приложено во время откачки воды из котлована. Вода, как правило, откачивается на ту глубину, которой будет достаточно для того, чтобы появилась возможность установить ярус креплений. Она составляет, по крайней мере, 1,5 метра.
Также необходимо учитывать и виды шпунтовых ограждений.
При расчете шпунтового ограждения, вбиваемого в водонепроницаемые грунты (глины и суглинок), которые расположены ниже горизонта воды, следует учитывать также и горизонтальные нагрузки.
Оценка влияния строительства на окружающую застройку.
Октябрь 2015 годаВ условиях плотной существующей застройки, необходимо правильно оценивать риски связанные с подвижкой грунтов и осадкой соседних зданий во время нового строительства. В статье мы покажем методику расчета на примере обустройства котлована в плотной исторической застройке.
В настоящее время существуют достаточно разработанные методики оценки влияния нового строительства на окружающие здания. Обычно методики достаточно дорогостоящие и требуют проведения изысканий по обследования несущей способности грунтов и конструкций прилегающих зданий.
Но иногда ситуация немного упрощается, когда проектировщики сталкиваются с ситуацией, расположения соседних зданий на границе влияния строительных работ. Пример расчета для такого случая мы приведем ниже.
ОЦЕНКА ВЛИЯНИЯ НОВОГО СТРОИТЕЛЬСТВА НА СУЩЕСТВУЮЩУЮ ЗАСТРОЙКУ
И РАСЧЕТ ЭЛЕМЕНТОВ КРЕПЛЕНИЯ КОТЛОВАНА
В первой Части статьи «Оценка влияния строительства на окружающую застройку» выполнены расчеты элементов крепления котлована при стадии откопки котлована -3,6 метра с установкой обвязочной балки. Но расчеты показали, что прочность конструкции недостатоточная и требуется дополнительное усиление.
Но расчеты показали, что прочность конструкции недостатоточная и требуется дополнительное усиление.
3.4. Стадия откопки 3,6 м. Обвязочная балка 40К1. Предусмотрены дополнительные угловые распорки из трубы 530х10.
Расчеты показывают, что максимальные горизонтальные перемещения шпунтовой стены 6 см.
Изгибающий момент в шпунтовой стене показан ниже:
Момент сопротивления 1м стенки Wo, см3/м VL606A(S 355 GP) 1800 см3/м
M/W= < 920000 кг*см/м /1800 см3/м =511кг/см2 < 3550*0.95 =3373 кг/см2
3.5. Изгибающий момент в обвязочной системе:
Расчет обвязочной балки по прочности:
Сталь: C255
Группа конструкций по приложению В СП 16.13330.2011 2
Коэффициент надежности по ответственности 0.95
Коэффициент условий работы 1
Предельная гибкость для сжатых элементов: 200
Предельная гибкость для растянутых элементов: 300
СЕЧЕНИЕ:
Геометрические характеристики
|
|
Параметр |
Значение |
Единицы измерения |
|
A |
Площадь поперечного сечения |
186. |
см2 |
|
Av,y |
Условная площадь среза вдоль оси U |
98.279 |
см2 |
|
Av,z |
Условная площадь среза вдоль оси V |
40.073 |
см2 |
|
a |
Угол наклона главных осей инерции |
0 |
град |
|
Iy |
Момент инерции относительно центральной оси Y1 параллельной оси Y |
56146. |
см4 |
|
Iz |
Момент инерции относительно центральной оси Z1 параллельной оси Z |
18921.9 |
см4 |
|
It |
Момент инерции при свободном кручении |
193.376 |
см4 |
|
Iw |
Секториальный момент инерции |
6687756.314 |
см6 |
|
iy |
Радиус инерции относительно оси Y1 |
17. |
см |
|
iz |
Радиус инерции относительно оси Z1 |
10.064 |
см |
|
Wu+ |
Максимальный момент сопротивления относительно оси U |
2850.102 |
см3 |
|
Wu- |
Минимальный момент сопротивления относительно оси U |
2850.102 |
см3 |
|
Wv+ |
Максимальный момент сопротивления относительно оси V |
950. |
см3 |
|
Wv- |
Минимальный момент сопротивления относительно оси V |
950.849 |
см3 |
|
Wpl,u |
Пластический момент сопротивления относительно оси U |
3118.442 |
см3 |
|
Wpl,v |
Пластический момент сопротивления относительно оси V |
1440.792 |
см3 |
|
Iu |
Максимальный момент инерции |
56146. |
см4 |
|
Iv |
Минимальный момент инерции |
18921.9 |
см4 |
|
iu |
Максимальный радиус инерции |
17.337 |
см |
|
iv |
Минимальный радиус инерции |
10.064 |
см |
|
au+ |
Ядровое расстояние вдоль положительного направления оси Y(U) |
5. |
см |
|
au- |
Ядровое расстояние вдоль отрицательного направления оси Y(U) |
5.09 |
см |
|
av+ |
Ядровое расстояние вдоль положительного направления оси Z(V) |
15.257 |
см |
|
av- |
Ядровое расстояние вдоль отрицательного направления оси Z(V) |
15.257 |
см |
|
P |
Периметр |
232. |
см |
Длина элемента 3 м
Расчетная длина в плоскости XoY 1
Расчетная длина в плоскости XoZ 1
Расстояние между точками раскрепления из плоскости 1 м
Результаты расчета по комбинациям загружений
N = 0 Т
My = 42 Т*м
Qz = 1 Т
Mz = 0 Т*м
Qy = 0 Т
|
Проверено по СНиП |
Проверка |
Коэффициент использования |
|
п. |
Прочность при действии изгибающего момента My |
0.572 |
|
п.8.2.1 |
Прочность при действии поперечной силы Qz |
0.017 |
|
п.9.1.1 |
Прочность при совместном действии продольной силы и изгибающих моментов с учетом пластики |
0.545 |
|
п.8.4.1 |
Устойчивость плоской формы изгиба |
0.572 |
|
п.10.4.1 |
Предельная гибкость в плоскости XoY |
0. |
|
п.10.4.1 |
Предельная гибкость в плоскости XoZ |
0.058 |
Коэффициент использования 0.572 — Прочность при действии изгибающего момента My
КРИВЫЕ ВЗАИМОДЕЙСТВИЯ
|
Фиксированные значения усилий |
Qz = 0 Т |
|
Область изменения усилий |
-455.032 Т < N < 481.22 Т |
Отчет сформирован программой Кристалл (32-бит), версия: 11.5.*.* от 01.01.2013
3.6. ОЦЕНКА ВЛИЯНИЯ НА ОКРУЖАЮЩУЮ ЗАСТРОЙКУ
Горизонтальные перемещения:
Вертикальные перемещения:
В соответствии с ТСН 50-302-2004 и ВСН 490-87 для зданий окружающей застройки допустимые параметры дополнительных деформаций составляют:
|
Категория технического состояния |
Предельно допустимые дополнительные деформации |
Допустимые ускорения колебаний, м/с2 |
||
|
Вертикальные перемещения (осадка), мм |
Относительная разность осадок |
крен |
||
|
II |
30 |
0,0015 |
0,002 |
0,15 |
|
III |
20 |
0,001 |
0,002 |
0,15 |
Согласно расчетам, на расстоянии 15м от бровки котлована отсутствует какое-либо влияние.
4. ВЫВОДЫ
Выполнен расчет ограждения котлована.
Приняты следующие этапы производства работ:
1. Погружение шпунта
2. Стадия откопки 2 м (абс. 4,600). Без крепления откосов. Установка обвязочной балки 40К1. Монтаж угловых распорок из прямошовной электросварной трубы 530х10.
3. Стадия откопки 3,6 м (абс. 3,000) м.
В качестве ограждения котлована применен шпунт VL 606A (или аналог). Принята отметка откопки котлована 3,000. При данной схеме конструкция шпунтового ограждения отвечает требованиям прочности, деформативности и устойчивости.
На расстоянии 15м от бровки котлована отсутствует какое-либо влияние.
Рекомендуется при производстве работ избежать дополнительных нагрузок на бровку котлована. Динамическое воздействие от оборудования для погружения шпунта подобрать с учетом минимального воздействия на грунты.
Необходимо вести постоянный мониторинг за перемещением шпунтового ограждения.
Подготовлено по материалам компании «Питер Девелопмент». При перепечатке ссылка обязательна.
При перепечатке ссылка обязательна.
Устройство шпунтового ограждения, цена 500 руб./пог.м в Москве и области
Наша организация обладает всем необходимым парком строительной техники для выполнения работ по устройству шпунтового ограждения котлованов.
Выполняем шпунт любым методом и любой сложности. При отсутствии проекта у заказчика мы имеем возможность создать нужный проект и выполнить работы по нему.
Многолетний опыт работ позволяет нам находить решения даже в самых сложных ситуациях. Наши специалисты с удовольствием проконсультируют вас. Опыт работы с 2007 года!
А также извлекаем из земли и покупаем трубы шпунтового ограждения.
Как мы работаем
Пример устройства шпунтового ограждения при помощи экскаватора с навесным оборудованием: гидровращатель «бочка» и гидравлический вибропогружатель
Преимущество нашей компании
Опыт работы с 2007 | Своя спецтехника | ||
Профессиональные сотрудники | Доступные цены |
Компания «СК Большая Медведица» специализируется на демонтаже зданий и подготовке строительных площадок для проведения дальнейших работ. Мы используем уникальную инновационную технику, поэтому проводим работы быстро и качественно. Получить более подробную информацию по спектру услуг, предлагаемых компанией, их стоимости и сроках проведения работ можно по телефонам, указанным в разделе «Контакты» или электронной почте.
Подпорная стена из шпунта [в качестве опоры]
Подпорная стена из шпунта широко используется в строительном секторе благодаря своей доступности и простоте использования в строительстве.
Шпунтовые сваи используются в качестве постоянных конструкций для защиты прилегающих конструкций. Это позволяет избежать перемещения грунта вблизи фундамента, особенно при наличии очень слабого грунта. Кроме того, подпорная стенка из шпунта используется в качестве подпорки при земляных работах и т. д.
В методике, упомянутой в разделе «Конструкционный анализ», разработан метод расчета необходимой длины шпунтовой сваи для удержания вынутого грунта.
КОНСТРУКЦИОННЫЙ АНАЛИЗДоступен общий метод анализа и проектирования подпорной стенки из шпунта, который учитывается при проектировании для проверки требуемой длины шпунтовых свай.
Процедура проектирования, описанная в книге Принципы проектирования фундаментов Браджа М. Даса предназначена для структурного анализа и проектирования.
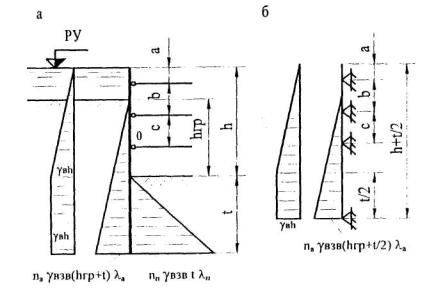
На рисунке 01 показано расположение шпунта, заглубленного в грунт, и характер его деформации.
Рисунок 01: Приложение давления грунта на шпунтовую сваю, заглубленную в землю
Изменение давления грунта на стенку шпунта показано на рисунке 2. стенки и изменение изгибающего момента, необходимое для нахождения модуля сечения шпунтовой сваи, указаны на рис. 2. шпунтовых свай для удержания котлована.
стенки и изменение изгибающего момента, необходимое для нахождения модуля сечения шпунтовой сваи, указаны на рис. 2. шпунтовых свай для удержания котлована.
Рисунок 02: Изменение вязкого момента в шпунтовой свае
ПРИМЕР РАБОТЫ ПРЕДПОЛОЖЕНИЯ И ПАРАМЕТРЫПри анализе и проектировании учитывались следующие предположения и расчет.
Высота до водного стола от готового уровня земли 1.5M
- плотность бетона 25 кН / м 3
- плотность почвы 18 кН / м 3 ·
- плотность насыщенной почвы 20 кН / м 3
- Плотность погруженной почвы 10 кН / м 3
- плотность воды 10 кН / м 3
- Угол трения почвы 30 0
Анализ структуры был выполнен в соответствии с описанной ранее процедурой.
Расчет бокового давления грунта путем расчета соответствующих параметров и оценки длины шпунтовой сваи выполняется в этом разделе.
Учитывая состояние слоя грунта, в этом расчете принимается средний угол трения.
Расчет бокового коэффициента давления наземного давленияугол трения почвы = 30 0
KA = (1-SIN Φ ) / 1 + SIN Φ )
= (1-грех 30) / 1+Sin 30 )
= 0.333
кП = (1 + SIN Φ ) / 1-SIN Φ )
= (1 + SIN 30) / 1-SIN 30)
= 3.000
Глубина проникновения = L 4 + L 3
= 3.368 + 0.524
= 3,892 м
= 3,892 м
Общая длина листа Куча = L 1 + L 2 + L 3 + L 4
= 1,5 + 1,5 + 3.368 + 0,524
= 6 .892 м
Минимальная необходимая длина шпунта составляет 6,892 м. Для строительства можно использовать шпунтовые сваи длиной 9 м. Если для строительства будут использоваться шпунтовые сваи длиной 9 м, то коэффициент запаса прочности будет равен 1,3.
Для строительства можно использовать шпунтовые сваи длиной 9 м. Если для строительства будут использоваться шпунтовые сваи длиной 9 м, то коэффициент запаса прочности будет равен 1,3.
В статье конструкция подпорной стены приведен метод расчета устойчивости нормальной бетонной стены, который является более простым, чем рассмотренный в этой статье.
Онлайн-курсы PDH.PDH для профессиональных инженеров. ПДХ Инжиниринг.
«Мне нравится широта ваших курсов HVAC; не только экологичность или энергосбережение
курсы.»
Рассел Бейли, ЧП
Нью-Йорк
«Это укрепило мои текущие знания и научило меня еще нескольким новым вещам
для раскрытия мне новых источников
информации.»
Стивен Дедак, ЧП
Нью-Джерси
«Материал был очень информативным и организованным. Я многому научился, и они были
Я многому научился, и они были
очень быстро отвечают на вопросы.
Это было на высшем уровне. Буду использовать
еще раз. Спасибо.»
Блэр Хейворд, ЧП
Альберта, Канада
«Легкий в использовании веб-сайт.Хорошо организовано. Я действительно воспользуюсь вашими услугами снова.
Я передам вашу компанию
имя другим на работе.»
Рой Пфлейдерер, ЧП
Нью-Йорк
«Справочный материал был превосходным, и курс был очень информативным, тем более что я думал, что уже знаком
с реквизитами Канзас
Авария в городе Хаятт.»
Майкл Морган, ЧП
Техас
«Мне очень нравится ваша бизнес-модель. Мне нравится возможность просмотреть текст перед покупкой. Я нашел класс
информативный и полезный
на моей работе. »
»
Уильям Сенкевич, Ч.Е.
Флорида
«У вас большой выбор курсов и очень информативные статьи.Вы
— лучшее, что я нашел.»
Рассел Смит, ЧП
Пенсильвания
«Я считаю, что такой подход позволяет работающему инженеру легко зарабатывать PDH, предоставляя время для проверки
материал.»
Хесус Сьерра, ЧП
Калифорния
«Спасибо, что разрешили мне просмотреть неправильные ответы.На самом деле
человек узнает больше
от сбоев.»
Джон Скондрас, ЧП
Пенсильвания
«Курс был хорошо составлен, и использование тематических исследований является эффективным
способ обучения.»
Джек Лундберг, ЧП
Висконсин
«Я очень впечатлен тем, как вы представляете курсы; т. э., что позволяет
э., что позволяет
студент для ознакомления с курсом
материал перед оплатой и
получение викторины.»
Арвин Свангер, ЧП
Вирджиния
«Спасибо, что предложили все эти замечательные курсы. Я, конечно, выучил и
очень понравилось.»
Мехди Рахими, ЧП
Нью-Йорк
«Я очень доволен предлагаемыми курсами, качеством материалов и простотой поиска и
подключение к Интернету
курсы.»
Уильям Валериоти, ЧП
Техас
«Этот материал в значительной степени оправдал мои ожидания. Курс был легким для понимания. Фотографии в основном давали хорошее представление о
обсуждаемые темы.»
Майкл Райан, ЧП
Пенсильвания
«Именно то, что я искал. Нужен 1 балл по этике, и я нашел его здесь.»
Нужен 1 балл по этике, и я нашел его здесь.»
Джеральд Нотт, ЧП
Нью-Джерси
«Это был мой первый онлайн-опыт получения необходимых кредитов PDH. Это был
информативно, выгодно и экономично.
Очень рекомендую
всем инженерам.»
Джеймс Шурелл, ЧП
Огайо
«Я ценю, что вопросы «реального мира» и имеют отношение к моей практике, и
не основано на каком-то непонятном разделе
законов, которые не применяются
до «обычная» практика.»
Марк Каноник, ЧП
Нью-Йорк
«Отличный опыт! Я многому научился, чтобы использовать его в своем медицинском устройстве
организация.»
Иван Харлан, ЧП
Теннесси
«Материал курса имеет хорошее содержание, не слишком математический, с хорошим акцентом на практическое применение технологии.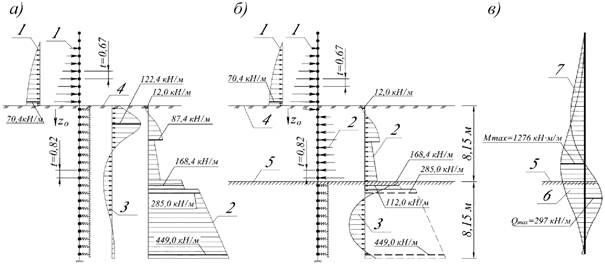 »
»
Юджин Бойл, П.Е.
Калифорния
«Это был очень приятный опыт. Тема была интересной и хорошо представлена,
а онлайн формат был очень
доступно и просто
использование. Большое спасибо.»
Патрисия Адамс, ЧП
Канзас
«Отличный способ добиться соответствия непрерывному обучению PE в рамках временных ограничений лицензиата.»
Джозеф Фриссора, ЧП
Нью-Джерси
«Должен признаться, я действительно многому научился. Распечатанная викторина помогает во время
просмотр текстового материала. я
также оценил просмотр
предоставлены фактические случаи.»
Жаклин Брукс, ЧП
Флорида
«Документ Общие ошибки ADA в проектировании помещений очень полезен.
тест действительно требовал исследований в
документ но ответы были
всегда в наличии.»
Гарольд Катлер, ЧП
Массачусетс
«Это было эффективное использование моего времени. Спасибо за разнообразие выбора
в дорожной технике, который мне нужен
для выполнения требований
Сертификация PTOE.»
Джозеф Гилрой, ЧП
Иллинойс
«Очень удобный и доступный способ заработать CEU для выполнения моих требований в штате Делавэр.»
Ричард Роудс, ЧП
Мэриленд
«Узнал много нового о защитном заземлении. До сих пор все курсы, которые я проходил, были отличными.
Надеюсь увидеть больше 40%
курсы со скидкой.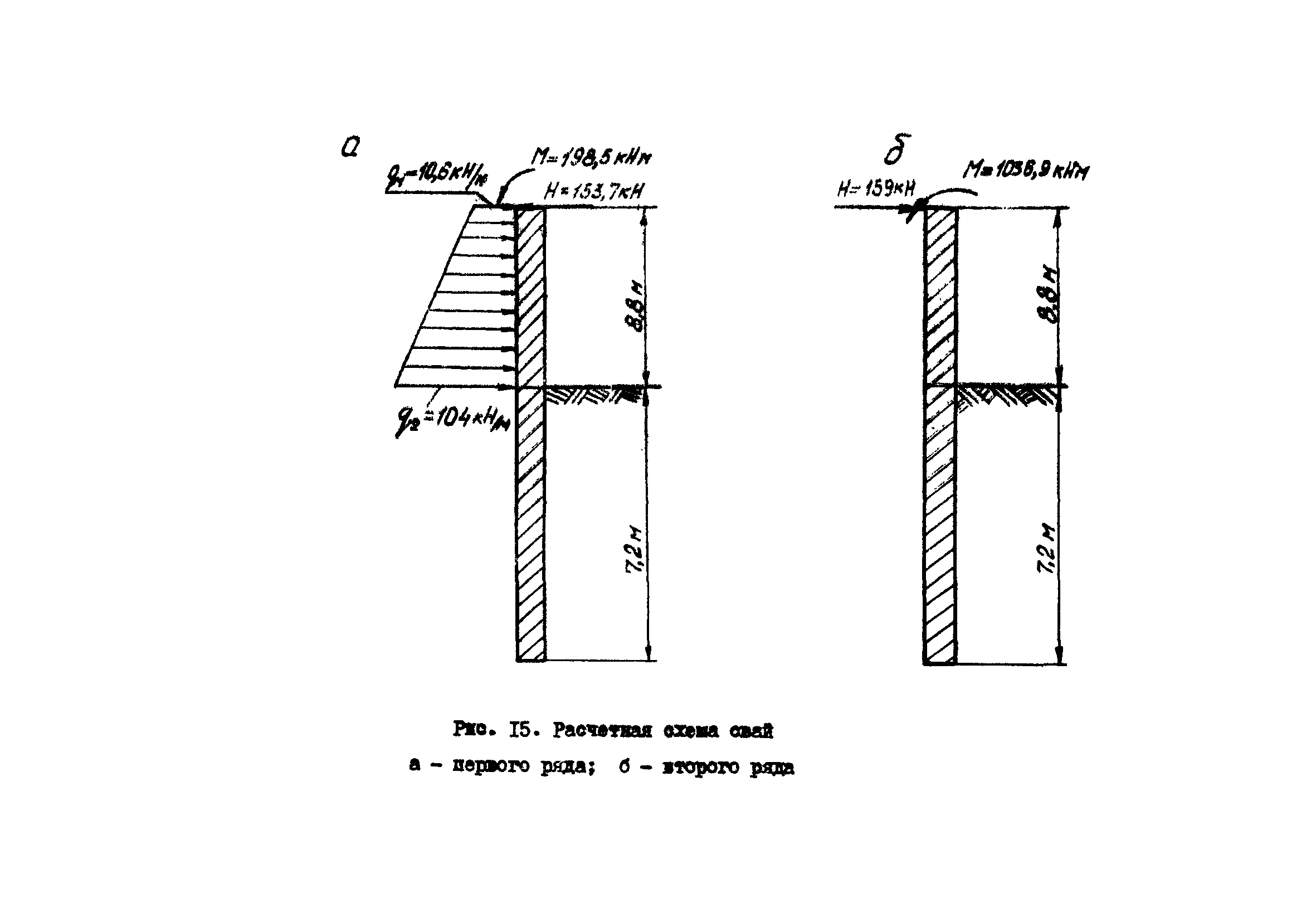 »
»
Кристина Николас, ЧП
Нью-Йорк
«Только что сдал экзамен по радиологическим стандартам и с нетерпением жду дополнительных
курсы. Процесс прост, и
намного эффективнее, чем
необходимость путешествовать.»
Деннис Мейер, ЧП
Айдахо
«Услуги, предоставляемые CEDengineering, очень полезны для профессионалов
Инженеры для приобретения блоков PDH
в любое время.Очень удобно.»
Пол Абелла, ЧП
Аризона
«Пока все было отлично! Поскольку я постоянно работаю матерью двоих детей, у меня не так много
пора искать куда
получить мои кредиты от.»
Кристен Фаррелл, ЧП
Висконсин
«Это было очень информативно и поучительно. Легко понять с иллюстрациями
Легко понять с иллюстрациями
и графики; определенно получается
проще впитать все
теорий.»
Виктор Окампо, P.Eng.
Альберта, Канада
«Хороший обзор принципов полупроводников. Мне понравилось проходить курс по телефону
.мой собственный темп во время моего утра
метро
на работу.»
Клиффорд Гринблатт, ЧП
Мэриленд
«Просто найти интересные курсы, загрузить документы и получить
викторина. Я бы очень рекомендую
вам в любой PE нуждающийся
Единицы CE.»
Марк Хардкасл, ЧП
Миссури
«Очень хороший выбор тем во многих областях техники. »
»
Рэндалл Дрейлинг, ЧП
Миссури
«Я заново узнал то, что забыл. Я также рад помочь финансово
от ваш рекламный адрес электронной почты который
сниженная цена
на 40%.»
Конрадо Касем, П.Е.
Теннесси
«Отличный курс по разумной цене. Буду пользоваться вашими услугами в будущем.»
Чарльз Флейшер, ЧП
Нью-Йорк
«Это был хороший тест, и я фактически проверил, что я прочитал профессиональную этику
Кодыи Нью-Мексико
правила.»
Брун Гильберт, П.Е.
Калифорния
«Мне очень понравились занятия. Они стоили времени и усилий. »
»
Дэвид Рейнольдс, ЧП
Канзас
«Очень доволен качеством тестовых документов. Буду использовать CEDengineerng
при необходимости дополнительного
Сертификация.»
Томас Каппеллин, П.Е.
Иллинойс
«У меня истек срок действия курса, но вы все равно выполнили обязательство и дали
мне то, за что я заплатил — много
спасибо!»
Джефф Ханслик, ЧП
Оклахома
«CEDengineering предлагает удобные, экономичные и актуальные курсы
для инженера.»
Майк Зайдл, П.Е.
Небраска
«Курс был по разумной цене, а материал был лаконичным и
хорошо организовано. »
»
Глен Шварц, ЧП
Нью-Джерси
«Вопросы соответствовали урокам, а материал урока
хороший справочный материал
для дизайна под дерево.»
Брайан Адамс, П.Е.
Миннесота
«Отлично, я смог получить полезные советы с помощью простого телефонного звонка.»
Роберт Велнер, ЧП
Нью-Йорк
«У меня был большой опыт прохождения программы «Строительство прибрежных зон — Проектирование»
Корпус Курс и
очень рекомендую.»
Денис Солано, ЧП
Флорида
«Очень понятный, хорошо организованный веб-сайт. Материалы курса этики штата Нью-Джерси были очень
прекрасно приготовлено. »
»
Юджин Брекбилл, ЧП
Коннектикут
«Очень хороший опыт. Мне нравится возможность скачивать учебные материалы на
обзор везде и
когда угодно.»
Тим Чиддикс, ЧП
Колорадо
«Отлично! Поддерживайте широкий выбор тем на выбор.»
Уильям Бараттино, ЧП
Вирджиния
«Процесс прямой, никакой чепухи. Хороший опыт.»
Тайрон Бааш, П.Е.
Иллинойс
«Вопросы на экзамене были пробными и демонстрировали понимание
материала. Тщательный
и полный.»
Майкл Тобин, ЧП
Аризона
«Это мой второй курс, и мне понравилось то, что курс предложил мне, что
поможет в моей линии
работы. »
»
Рики Хефлин, ЧП
Оклахома
«Очень быстрая и простая навигация. Я определенно воспользуюсь этим сайтом снова.»
Анджела Уотсон, ЧП
Монтана
«Прост в исполнении. Нет путаницы при подходе к сдаче теста или записи сертификата.»
Кеннет Пейдж, П.Е.
Мэриленд
«Это был отличный источник информации о нагреве воды с помощью солнечной энергии. Информативный
и отличное освежение.»
Луан Мане, ЧП
Коннетикут
«Мне нравится подход к подписке и возможности читать материалы в автономном режиме, а затем
вернись, чтобы пройти тест.»
Алекс Млсна, П.Е.
Индиана
«Я оценил количество информации, предоставленной для класса. Я знаю
это вся информация, которую я могу
использование в реальных жизненных ситуациях.»
Натали Дерингер, ЧП
Южная Дакота
«Материалы обзора и образец теста были достаточно подробными, чтобы я мог
успешно завершено
курс.»
Ира Бродская, ЧП
Нью-Джерси
«Веб-сайт прост в использовании, вы можете скачать материал для изучения, а затем вернуться
и пройти тест. Очень
удобный а на моем
собственное расписание.»
Майкл Гладд, ЧП
Грузия
«Спасибо за хорошие курсы на протяжении многих лет.»
Деннис Фундзак, ЧП
Огайо
«Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать PDH
сертификат . Спасибо за создание
Спасибо за создание
процесс простой.»
Фред Шайбе, ЧП
Висконсин
«Положительный опыт.Быстро нашел подходящий мне курс и закончил
PDH за один час в
один час.»
Стив Торкилдсон, ЧП
Южная Каролина
«Мне понравилась возможность загрузки документов для ознакомления с содержанием
и пригодность до
наличие для оплаты
материал .»
Ричард Ваймеленберг, ЧП
Мэриленд
«Это хорошее пособие по ЭЭ для инженеров, не являющихся электриками.»
Дуглас Стаффорд, ЧП
Техас
«Всегда есть место для улучшения, но я ничего не могу придумать в вашем
процесс, которому требуется
улучшение. »
»
Томас Сталкап, ЧП
Арканзас
«Мне очень нравится удобство прохождения викторины онлайн и получения немедленного
Сертификат.»
Марлен Делани, ЧП
Иллинойс
«Обучающие модули CEDengineering — очень удобный способ доступа к информации по
многие различные технические области снаружи
по собственной специализации без
необходимость путешествовать.»
Гектор Герреро, ЧП
Грузия
Глава 2. Конструктивный расчет стен из шпунтовых свай
Для получения полной версии этого документа щелкните здесь.
2.1. Материалы, используемые для шпунтовых свай
2.1.1. Марки шпунтовой стали
2. 1.1.1. Базовый класс: ASTM A-328
1.1.1. Базовый класс: ASTM A-328
Базовой спецификацией для стальных шпунтовых свай в Соединенных Штатах является стандарт ASTM A-328, опубликованный Американским обществом по испытанию материалов.Этот сорт был удовлетворительным для большинства применений, поскольку он обеспечивал относительно высокий предел текучести для конструкции и высокий предел прочности для управляемости. Состав не очень хорошо подходит для сварки, хотя процедуры сварки этого сорта были опубликованы или доступны у производителей. Сталь не особенно прочная, и были отмечены трещины, возникающие в местах надрезов, особенно в холодных условиях. Эта сталь имеет минимальный предел текучести 39 тысяч фунтов на квадратный дюйм и минимальную прочность на растяжение 70 тысяч фунтов на квадратный дюйм.
2.1.1.2. Высший класс прочности: ASTM A-572
Стали более высокой прочности для конструкционных применений доступны для шпунтовых свай, таких как серия ASTM A-572. Не у каждого производителя могут быть доступны все прочности, однако почти всегда предлагается класс 50. Высокопрочные марки находят применение (1) для замены более легкой секции более высокой прочности на более тяжелую секцию обычной прочности, (2) для поддержания коэффициентов запаса по пределу текучести, когда этого нельзя достичь с помощью модуля прочности сечения.Высокопрочные марки могут поддерживать некоторый запас прочности в отношении предела текучести, когда коррозия может снизить свойства сечения. Высокопрочные стали, как правило, лучше поддаются сварке, чем высокоуглеродистые.
Высокопрочные марки находят применение (1) для замены более легкой секции более высокой прочности на более тяжелую секцию обычной прочности, (2) для поддержания коэффициентов запаса по пределу текучести, когда этого нельзя достичь с помощью модуля прочности сечения.Высокопрочные марки могут поддерживать некоторый запас прочности в отношении предела текучести, когда коррозия может снизить свойства сечения. Высокопрочные стали, как правило, лучше поддаются сварке, чем высокоуглеродистые.
ASTM A-572 Grade 50 имеет минимальный предел текучести 50 тысяч фунтов на квадратный дюйм и минимальную прочность на растяжение 70 тысяч фунтов на квадратный дюйм. Коэффициенты безопасности для высокопрочных сталей аналогичны более низким классам прочности. Теперь он доступен в виде мелкозернистой смеси, убитой кремнием, со значительно улучшенными ударными характеристиками по Шарпи с V-образным надрезом.Эту сталь можно рассматривать для критических применений (например, строительство в арктических регионах) и конструкций, подверженных ударам. Это препарат премиум-класса.
Это препарат премиум-класса.
2.1.1.3. Класс коррозионной стойкости: ASTM A-690
МаркаASTM-A-690 была разработана для распознавания стали со специальным составом для шпунтовых и двутавровых свай, используемых в условиях соленой воды. Этот сорт продемонстрировал преимущества по сравнению с обычными углеродистыми сталями в отношении сопротивления коррозии в зоне брызг соленой воды, что вызывает озабоченность.Сталь также обеспечивает минимальный предел текучести 50 тысяч фунтов на квадратный дюйм и, следовательно, может быть разработана по аналогии со сталями A-572. В некоторых случаях вес может быть уменьшен, что обеспечивает экономию, которая компенсирует часть дополнительных затрат на сорт. Более подробное обсуждение этого материала представлено в 17.4.4.1.
2.1.1.4. Конструктивные факторы безопасности для стальных шпунтовых свай
Большинство стальных шпунтовых свай по-прежнему проектируются с использованием методов расчета допустимых напряжений; таким образом, обычно указывается коэффициент запаса, который уменьшает допустимое напряжение в свае от предела текучести. Таким образом, допустимое напряжение равно
Таким образом, допустимое напряжение равно
Уравнение 2-1: σallow = Freduction σy
где
- σallow = Допустимое напряжение материала
- Freduction = Понижающий коэффициент безопасности
- σy = предел текучести материала, фунт/кв. дюйм или кПа
Для стальных свай при чистом изгибе (см. ниже) используются два понижающих коэффициента:
Для статических нагрузок, для постоянных работ коэффициент снижения обычно составляет 0,65, или допустимое напряжение составляет 65% от предела текучести.Для классов, перечисленных выше:
ASTM A328: σразреш = (0,65)(39) ≈ 25 тысяч фунтов/кв. дюйм
ASTM A572, ASTM A690: σразреш = (0,65)(50) ≈ 32,5 тысяч фунтов/кв. дюйм
Для сейсмических нагрузок коэффициент уменьшения обычно составляет (1,33)(0,65) ≈ 0,87, или допустимое напряжение составляет 87% от предела текучести. Использование этого повышенного значения для сейсмических нагрузок предполагает статический анализ, чтобы гарантировать, что статический случай фактически не является определяющим для конкретной ситуации (см. Пример 19). Для классов, перечисленных выше:
Пример 19). Для классов, перечисленных выше:
ASTM A328: σразрешить = (0.87)(39) ≈ 34 тысяч фунтов на квадратный дюйм
ASTM A572, ASTM A690: σразреш = (0,87)(50) ≈ 43,5 тысяч фунтов/кв. дюйм
2.1.2. Прочие материалы
Алюминий, используемый в шпунтовых сваях, обычно такой же, как и другие экструдированные алюминиевые профили. Свойства материала можно узнать у производителей, и они также подробно обсуждаются в книге «Забивка свай» автора Pile Buck. В той же книге более подробно обсуждается древесина; древесина greenheart, например, обладает отличными свойствами материала.
Виниловые и пултрузионные стекловолоконные сваи изготавливаются из материалов, свойства которых сильно различаются от производителя к производителю.Таким образом, при спецификации этих разделов очень важно проверить как механические свойства, так и метод, с помощью которого эти механические свойства были получены. Также важно отметить, что при использовании обоих этих материалов применение этих свойств материала зависит от многих факторов, таких как ползучесть (в случае виниловых секций), поперечный изгиб и локальное коробление (для обоих этих материалов).
2.2. Гибка шпунтовых свай
2.2.1. Теория чистого изгиба листов
Основной целью структурного анализа шпунтовых свай является анализ разрушения из-за избыточного изгибающего момента и напряжений. Большая часть анализа консольных и закрепленных стен включает расчет чистого изгиба. В случае чистого изгиба максимально допустимый изгибающий момент определяется уравнением
.Уравнение 2-2: Mallow = Smin σ разрешает
где
- Мальва = Допустимый изгибающий момент
- Smin = минимальный модуль упругости сечения
Как допустимый изгибающий момент, так и модуль сопротивления указаны в линейных футах или метрах стены.Прочность шпунтовых свай на изгиб зависит от формы профиля и материала, из которого он изготовлен. Допустимое напряжение материала зависит от самого материала.
2.2.2. Применение гибки к определенным секциям шпунтовых свай
Многовековое развитие шпунтовых свай привело к увеличению количества профилей всех видов. Они постоянно меняются; их таблица выходит за рамки этой книги, хотя они доступны как в печатной, так и в онлайновой форме на Pile Buck.Однако для целей примеров задач в этой книге мы будем использовать несколько часто используемых профилей, которые изготавливались из стали в течение многих лет. Они показаны в таблице 2-1.
Они постоянно меняются; их таблица выходит за рамки этой книги, хотя они доступны как в печатной, так и в онлайновой форме на Pile Buck.Однако для целей примеров задач в этой книге мы будем использовать несколько часто используемых профилей, которые изготавливались из стали в течение многих лет. Они показаны в таблице 2-1.
2.2.3. Комбинированные осевые и изгибные напряжения
Кроме того, шпунтовые сваи также могут подвергаться осевой нагрузке от таких источников, как бетонные оголовки свай наверху, осевые силы из-за вертикальной составляющей наклонного анкера и трения о грунт. Особенно в случае наголовников свай они могут вызвать коробление шпунтовых свай.Это можно вычислить, изменив уравнение 2-2 и найдя максимальное (или допустимое) напряжение:
Уравнение 2-3:
σmax = Paxial + Mmax + Paxial (δmax + ep) < σ A позволяет осевую Swall
Где
- Mmax = максимальный момент защитного покрытия
- Paxial = осевая нагрузка на обшивку
- Aaxial = площадь обшивки, подверженная осевым нагрузкам
- δmax = максимальное отклонение обшивки
- ep = эксцентриситет нагрузки относительно осевой линии настила
Этот тип нагрузки на шпунтовые сваи особенно важен для стен ГП и продемонстрирован в примере 24.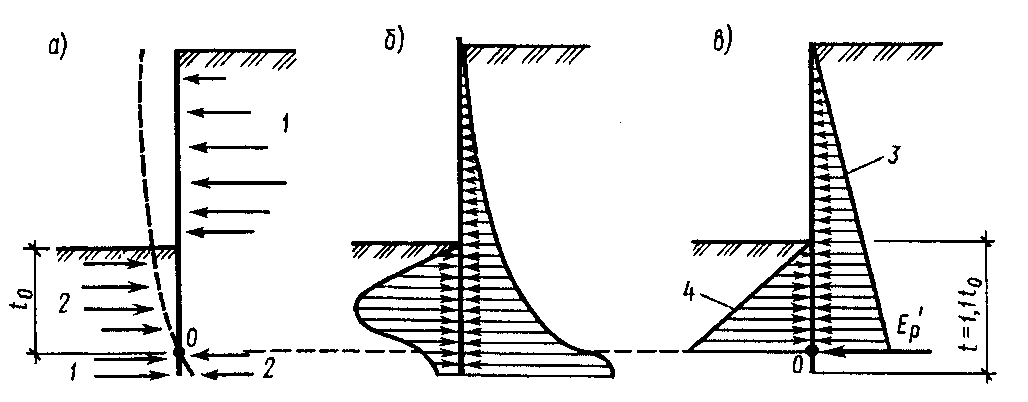
Рекомендуется, если не будет доказано, что коробление сваи маловероятно,
Уравнение 2-4: Mmax > Paxial ( δmax + ep ) 10
2.2.4. Модуль упругости U-образного листового проката
Как отмечалось выше, модуль упругости строго зависит от физической формы материала; однако со стальным листом Ларссен и Z-образные формы были связаны с давними различиями между европейской и американской практикой.
Larssen и другие U-образные сваи остаются популярными в Европе и на Дальнем Востоке, но в США они были вытеснены профилем Z-типа.Почему? В основе проблемы лежит различие в инженерной философии.
Как мы уже говорили, шпунтовые стены считаются балками. Для большинства форм нейтральная ось будет проходить посередине между двумя внешними сторонами листового материала, аналогично двутавровым балкам. В случае стены Ларсена линия замков приходится на нейтральную ось, а в случае Z-стены — нет. С момента создания сваи типа Ларсена, которая запирается вдоль нейтральной оси стены, возникла озабоченность по поводу способности замков передавать горизонтальный сдвиг, без которого нельзя развить полную прочность сечения.
Европейская философия была достаточно либеральна в этом отношении, и можно обнаружить, что модуль сечения, опубликованный для форм Ларсена, всегда основан на полном переносе или «комбинированном базисе» с редукцией из этого состояния, предоставленной инженеру.
Большинство американских инженеров придерживались более консервативного подхода и предположили, что, поскольку на этот перенос нельзя рассчитывать без сварки стыков, модуль сопротивления стены с блокировками на нейтральной оси должен основываться на свойствах одиночной сваи, а не комбинированная свайная система.Эта философия, конечно же, способствовала развитию форм Z-типа, которые смыкаются на гранях стены, где горизонтальный сдвиг равен нулю.
На самом деле существует общее мнение, что в блокировках всегда достигается некоторая фиксация, начиная со 100 процентов и ниже. Американский подход часто приводил к многократному увеличению запаса прочности и неэкономичному использованию материала. Европейский метод, возможно, время от времени давал некоторые предельные коэффициенты безопасности, но, по-видимому, было зарегистрировано мало фактических отказов.
Серия арочных шпунтовых свай малой глубины была разработана индустрией холодной отделки. Эти секции, по большей части, смыкаются со своими соседями на одной грани стены, вдали от нейтральной оси. Вопросы, поднятые в предыдущем абзаце, не относятся к этим формам, и опубликованный модуль сечения может использоваться аналогично Z-образным формам.
2.2.5. Разрушение при поперечном изгибе
Поперечный изгиб является относительно недавно признанным видом разрушения шпунтовых свай.Хотя он взаимодействует с классическим изгибом, это отдельный вид отказа.
Как мы видели, нагрузки на шпунтовые сваи возникают в основном за счет бокового давления грунта, которое, в свою очередь, вызывает сдвиги, моменты, повороты и отклонения в балке. В дополнение к изгибающей нагрузке, которая развивается вдоль оси шпунта, эти давления также действуют непосредственно на обшивку, создавая поперечную нагрузку, как показано на Рисунке 2-1. По сути, боковое давление сплющивает лист; изгиб пластины в углах является сопротивлением обшивки этому сплющиванию. Этот изгиб не зависит от классического изгиба, но комбинированные напряжения могут превышать пределы материала, даже если классический изгиб предсказывает обратное.
Этот изгиб не зависит от классического изгиба, но комбинированные напряжения могут превышать пределы материала, даже если классический изгиб предсказывает обратное.
Для получения полной версии этого документа щелкните здесь.
Базовая конфигурация анализа конструкции шпунтовой сваи
, Дон С. Уоррингтон, доктор философии, физкультура, Университет Теннесси в Чаттануге
Введение
Проектирование и анализ шпунтовых свай является важной частью инженерно-геологических работ и подробно описано в таких публикациях, как Проектирование шпунтовых свай Pile Buck .Появление программного обеспечения, такого как SPW 911 , значительно упростило выполнение этого проекта по сравнению с прошлым, когда для выполнения этой задачи использовались диаграммы и графические методы.
Но тот, кто не является обычным практикующим, может задаться вопросом: почему эта задача такая сложная? Почему мы не можем просто использовать некоторые формулы и покончить с этим? Цель этой статьи — показать, почему это так, и в то же время дать некоторое представление о том, как появились диаграммы, представленные в «Проектирование шпунтовых свай» от Pile Buck , и как мы, возможно, можем использовать эти упрощенные случаи, чтобы дать нам некоторое понимание конструкции шпунтовой сваи.
Консольные шпунтовые стены
Начнем с простейшего случая: консольная шпунтовая стена с однородной стратиграфией и без воды, которая может повлиять на результаты. Этот тип системы показан на рисунке 1:
Рис. 1 Базовая конфигурация (с номенклатурой) консольной шпунтовой стены в однородном грунтеПроще говоря, шпунтовые сваи поддерживаются пассивными давлениями ниже линии земснаряда, компенсирующими (либо при опрокидывании, либо скольжении) активные давления со стороны земли .Поскольку пассивный коэффициент давления грунта больше, чем активный, расстояние d, которое меньше, чем h+d активной стороны, может обеспечить это, если d допускается на достаточную глубину. Для этого анализа будет использоваться «упрощенный метод», который исключает инверсию активных и пассивных давлений в подошве стены, которые анализируются в «традиционном методе». Это тот же метод, который используется SPW 911.
Давайте определим некоторые переменные, сначала отношение коэффициента давления грунта:
Уравнение 1 Это используется в диаграммных решениях, представленных в Проектирование шпунтовых свай Pile Buck . Следующим является безразмерная высота ниже вершины стены, или
Следующим является безразмерная высота ниже вершины стены, или
Последнее, что мы имеем, это отношение проникновения настила ниже линии земснаряда к высоте выше, или
Уравнение 3Безразмерный момент в любой точке ниже линии земснаряда равен
Уравнение 4d’ (и, следовательно, d ), которую мы ищем, — это точка, в которой момент равен нулю, т. е. в носке сваи. Если мы получим действительный корень этого уравнения, а затем решим для d’ , мы получим
Уравнение 5Мы можем видеть, что глубина проникновения ниже линии земснаряда зависит здесь только от двух вещей: высоты обшивки над линией земснаряда (уравнение 3) и соотношения пассивного и активного давления грунта (уравнение 1.) Это подчеркивает наше описание основного принципа стен из шпунтовых свай.
Еще одним важным параметром является максимальный момент. Если мы возьмем производную уравнения 4 и приравняем ее к нулю, мы получим положение точки нулевого сдвига или максимального момента. Это положение o (и его безразмерный аналог o’ ) задается уравнением
Это положение o (и его безразмерный аналог o’ ) задается уравнением
Подстановка этого результата в уравнение 4 и определение его размеров дает максимальный момент,
Уравнение 7Количество за пределами дроби знакомо пользователям диаграмм в Дизайн шпунтовых свай от Pile Buck .Диаграмма, аналогичная показанной там, представлена на рисунке 2.
Рисунок 2 Диаграмма, показывающая зависимость d’, o’ и безразмерного максимального момента для консольных стенокМы можем рассмотреть примерную задачу следующим образом:
- Сухая консольная стена, однородный несвязный грунт, ровная засыпка, условия Ренкина
- φ = 30°, γ = 109,2 фунта на фут
- ч = 10’
- Пассивное снижение коэффициента запаса прочности = 1,5. Этот метод применения коэффициента безопасности объясняется в документе «Проектирование шпунтовых свай» Pile Buck .
Нам нужно найти проникновение ниже линии земснаряда d и максимальный момент на обшивке.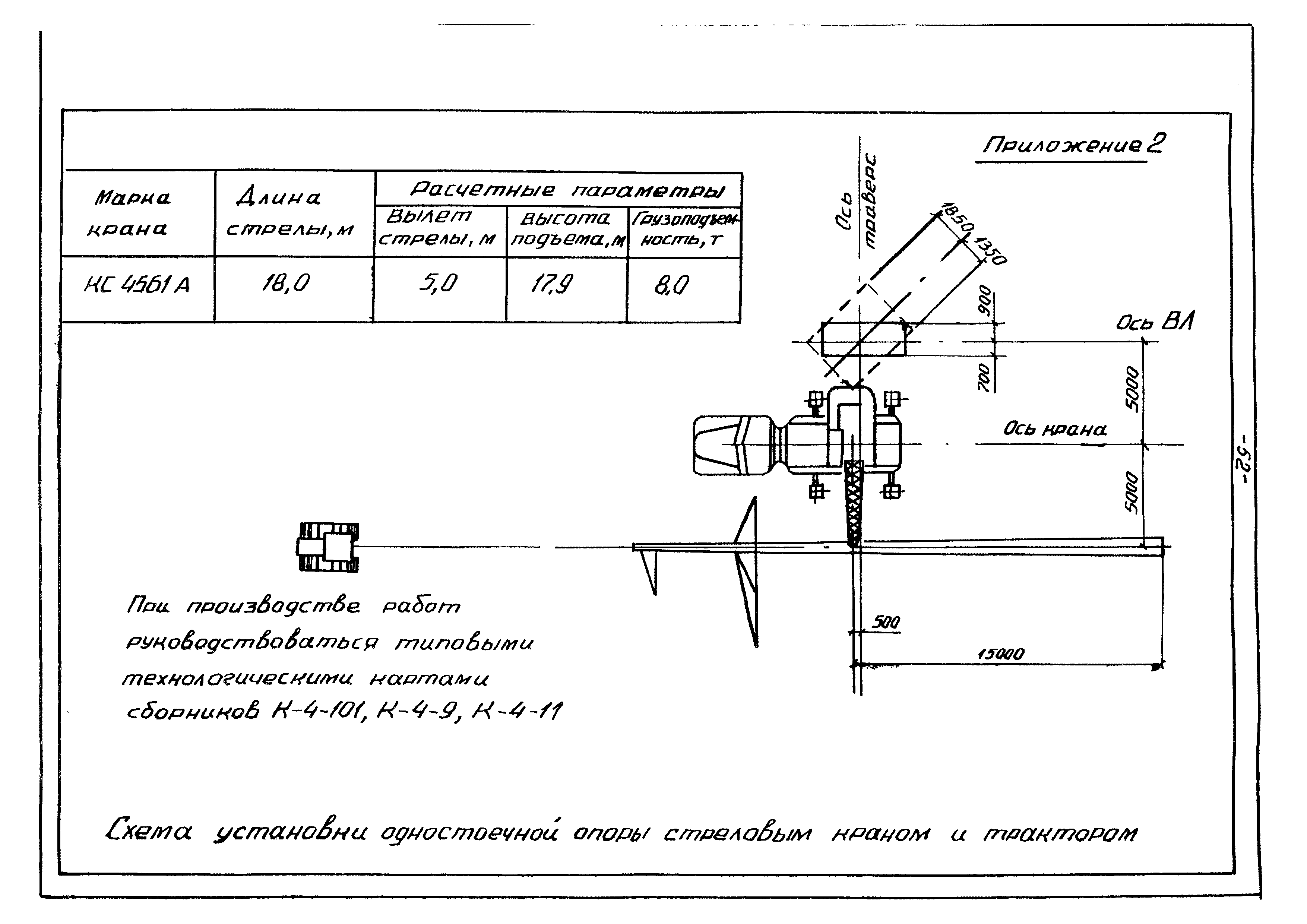
- Из теории Ренкина К a = 1/3 и К p = 3.
- Однако, поскольку мы должны уменьшить K p для коэффициента запаса, K p = 3/1,5 = 2. Отсюда κ = 2/(1/3) = 6.
- Подставляя это в уравнение 5, d’ = 1.22, и, таким образом, из уравнения 3 d = (1,22)(10’) = 12,2’.
- Упрощенный метод требует увеличения d . Дизайн шпунтовых свай от Pile Buck и интерактивная справка по SPW 911 объясняют, как это правильно применять. Для наших целей мы еще больше упростим процесс, увеличив всю проходку ниже линии земснаряда на 20%, таким образом, d = 12,2 + (0,2)(12,2) = 14,6’.
- Общая длина стены из шпунта составляет h + d = 10’ + 14.6’ = 24,6’.
- Подстановка переменных в уравнение 7 дает максимальный момент 17 325 фут-фунт/фут стены.
Этот результат можно сравнить с выводом SPW 911, который дает результат, показанный на рисунке 3.
Результаты SPW 911 мало отличаются от результатов решения закрытой формы. Наибольшая разница наблюдается при проникновении ниже линии земснаряда, что было объяснено выше.
Стены из анкерного шпунта
Добавление анкера к стене усложняет анализ.Схема этого показана на рисунке 4.
Рис. 4 Схема стены из шпунта с анкерным креплением (из Verruijt and van Bars (2007))Следующее также появляется в Verruijt and van Bars (2007), за исключением того, что некоторые номенклатуры отличаются.
В дополнение к переменным, определенным ранее, мы определяем
Уравнение 8Одним из недостатков схемы анкерных стен, приведенной в документе «Проектирование шпунтовых свай» от Pile Buck , является то, что она ограничена стенами с a’ = 0,25.
Отношение расстояния проникновения d’ является решением уравнения
Уравнение 9 Как и в случае с уравнением 4, это кубическое уравнение; однако решение значительно сложнее во всех смыслах этого слова.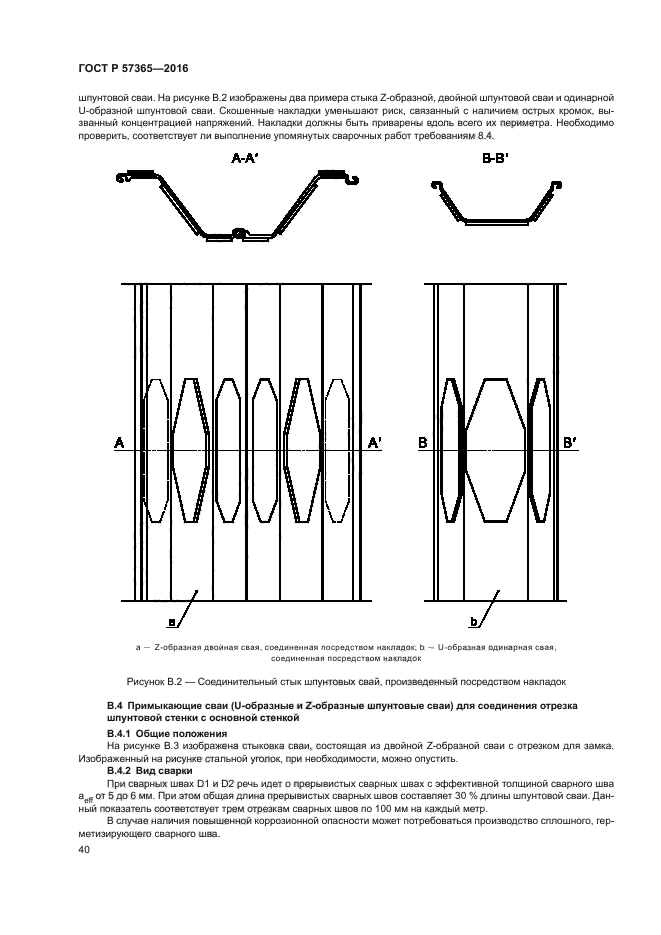 Самый простой способ решить это численно. Практически все электронные таблицы, например, имеют функцию поиска цели, которую можно использовать для решения этого уравнения. Кроме того, на рисунке 5 показана диаграмма, показывающая отношение a’ к d’ для различных значений κ .
Самый простой способ решить это численно. Практически все электронные таблицы, например, имеют функцию поиска цели, которую можно использовать для решения этого уравнения. Кроме того, на рисунке 5 показана диаграмма, показывающая отношение a’ к d’ для различных значений κ .
В любом случае отношение усилия анкера T к общему действующему давлению грунта на стенку шпунтовой сваи определяется уравнением
Уравнение 10Диаграмма, иллюстрирующая это соотношение (с использованием той же схемы осей, что и на рис. 5), показана на рис. 6.
Рис. 6. Значения коэффициента растяжения анкера для различных значений a’ (абсцисса) и κ (обозначение)Максимальный момент определяется (с использованием процедуры, аналогичной той, которая используется для консольных стен) с использованием уравнения
Уравнение 11 Результаты этого уравнения показаны на рисунке 7.
Безразмерный максимальный момент определяется уравнением
Уравнение 12Это показано на рисунке 8.
Рисунок 8. Значения безразмерного максимального местоположения для различных значений a’ (абсцисса) и κ (обозначение) со стены.Это дает a’ = 0,25. Безразмерные соотношения, полученные из приведенных выше уравнений, следующие:- d’ = 0,516 (уравнение 9)
- Коэффициент тяги анкера = 0,305 (уравнение 10)
- z’ для максимального момента = 0,836 (уравнение 11)
- Коэффициент момента = 0,108 (уравнение 12)
Подстановка, фактические параметры, которые получаются в результате следующие:
- г = 5,16’
- Т = 1274.6 фунтов/фут стены
- z = 8,37’
- M макс. = 3924,5 фут-фунт/фут
Их можно сравнить с результатами SPW 911, показанными на рисунке 9. Результаты очень близки.
Результаты очень близки.
. Обсуждение
.Сравнение консольных и анкерных решений показывает разницу между ними. Как и следовало ожидать, консольная стенка требует большего проникновения ниже линии земснаряда, чем анкерная.Однако максимальный момент в консольной стене (и, следовательно, сечение, необходимое для сопротивления ей) намного больше, чем у закрепленной стены. Это подчеркивает неотъемлемые преимущества анкерных стен, особенно для секций (таких как винил или стекловолокно), которые имеют низкий модуль сопротивления.
Имеются также некоторые комментарии, относящиеся к анкерным стенам и диаграммам, показанным на Рисунке 5–Рисунке 8.
Несмотря на то, что необходимое проникновение может быть уменьшено за счет понижения точки крепления, более существенным компромиссом является соотношение между максимальным моментом и моментом.тяга якоря. Чем ниже тяговое усилие якоря, тем ниже максимальный момент, но выше сила тяги якоря. Баланс этих двух параметров является важной частью конструкции стены из анкерного листа. Эти диаграммы не учитывают влияние опускания анкерной точки на область над анкерной точкой, где отклонения кантилевера могут быть значительными.
Баланс этих двух параметров является важной частью конструкции стены из анкерного листа. Эти диаграммы не учитывают влияние опускания анкерной точки на область над анкерной точкой, где отклонения кантилевера могут быть значительными.
Осмотр рис. 5 также показывает, что изменения коэффициента давления грунта κ оказывают большое влияние на глубину проникновения защитного покрытия, как это было в случае с консольными стенами.
Заключение
Следует отметить, что ни одно из этих уравнений не учитывает влияние вариаций стратиграфии почвы или присутствия воды. Отсутствие одного или обоих редко встречается в реальной конструкции шпунтовых свай. Сложность решения быстро возрастает при наличии любого из них, и в текущей практике необходимо использование программных пакетов, таких как SPW 911. Тем не менее, они полезны, возможно, в качестве «обратной стороны конверта» для оценки параметров проектирования шпунтовых свай и в качестве проверки результатов программного обеспечения, которое всегда полезно при геотехническом проектировании.
Каталожные номера
В дополнение к обширным ссылкам на Проектирование шпунтовых свай от Pile Buck и интерактивной справке по SPW 911, использовалась единственная ссылка Verruit and van Bars (2007), Soil Mechanics . Делфт, Нидерланды: VSSD.
Применение стальных шпунтовых свай для опоры мостов через воду в штате Небраска
Шпунтовые сваи рекомендуется устанавливать для большинства мостов, пересекающих воду, наряду с несущими сваями (например,г., обычно двутавровые или трубчатые сваи), чтобы избежать проблемы размыва и защитить грунт обратной засыпки в Небраске (раздел 4.1 БОПП). Шпунтовые сваи также часто применялись для полуинтегральных опорных мостов в Небраске. Хотя шпунтовые сваи не рекомендуются для сопротивления какой-либо вертикальной нагрузке в существующем БОПП, недавние исследования (Sylvain et al., 2017; Panchal et al., 2020) показали, что шпунтовые сваи можно использовать как для осевой несущей способности, так и для удержания обратной засыпки. для автомобильных мостов с короткими пролетами или с малой интенсивностью движения.Тем не менее, были ограниченные ресурсы с точки зрения проектирования, анализа (например, расчет вертикальной и поперечной несущей способности шпунтовых свай под такими надстройками) и стратегий строительства. С другой стороны, в Небраске имеется значительное количество короткопролетных мостов, которые в ближайшем будущем могут нуждаться в ремонте/замене. Согласно данным о мостах в Небраске из Datacenterhub (https://datacenterhub.org), в Небраске насчитывается 8 052 однопролетных моста из 17 717 обследованных мостов.А длина пролета 8 353 мостов меньше 70 футов. Многие из этих мостов были построены очень давно. Например, в 1930-х годах было построено около 3900 мостов, которые могут потребовать замены или ремонта/укрепления. Также было замечено, что значительная часть этих короткопролетных мостов расположена в восточной части штата из-за более мелких притоков реки Миссури. В связи с этим мы ожидаем в ближайшем будущем больших потребностей в ремонте мостов и замене этих мостов с короткими пролетами и/или мостами с низкой интенсивностью движения.
для автомобильных мостов с короткими пролетами или с малой интенсивностью движения.Тем не менее, были ограниченные ресурсы с точки зрения проектирования, анализа (например, расчет вертикальной и поперечной несущей способности шпунтовых свай под такими надстройками) и стратегий строительства. С другой стороны, в Небраске имеется значительное количество короткопролетных мостов, которые в ближайшем будущем могут нуждаться в ремонте/замене. Согласно данным о мостах в Небраске из Datacenterhub (https://datacenterhub.org), в Небраске насчитывается 8 052 однопролетных моста из 17 717 обследованных мостов.А длина пролета 8 353 мостов меньше 70 футов. Многие из этих мостов были построены очень давно. Например, в 1930-х годах было построено около 3900 мостов, которые могут потребовать замены или ремонта/укрепления. Также было замечено, что значительная часть этих короткопролетных мостов расположена в восточной части штата из-за более мелких притоков реки Миссури. В связи с этим мы ожидаем в ближайшем будущем больших потребностей в ремонте мостов и замене этих мостов с короткими пролетами и/или мостами с низкой интенсивностью движения. И многие из них являются водными мостами. Стальные шпунтовые сваи были определены как возможный вариант для этих короткопролетных или малогабаритных автодорожных мостов. Существует два основных способа использования шпунтовых свай в опорах моста: в качестве консольных стен или анкерных стен. Напротив, в США не так много проектов, в которых шпунтовые сваи с осевой нагрузкой использовались в устоях моста. В округах Небраски есть многобалочные (дощатые) мосты, установленные на несущих сваях с шпунтовыми сваями, используемыми в качестве опор.Однако эти шпунтовые сваи не обязательно несут балки или используются в качестве осевых элементов. Их скорее устанавливают для защиты грунтов засыпки и предотвращения размывания. Было отмечено, что необходимы более глубокие исследования из-за отсутствия опыта в отношении проектирования, анализа (например, сопротивления вертикальным и боковым нагрузкам), испытаний под нагрузкой и процедуры строительства в недавнем отчете по проекту Департамента транспорта штата Айова (Эванс).
И многие из них являются водными мостами. Стальные шпунтовые сваи были определены как возможный вариант для этих короткопролетных или малогабаритных автодорожных мостов. Существует два основных способа использования шпунтовых свай в опорах моста: в качестве консольных стен или анкерных стен. Напротив, в США не так много проектов, в которых шпунтовые сваи с осевой нагрузкой использовались в устоях моста. В округах Небраски есть многобалочные (дощатые) мосты, установленные на несущих сваях с шпунтовыми сваями, используемыми в качестве опор.Однако эти шпунтовые сваи не обязательно несут балки или используются в качестве осевых элементов. Их скорее устанавливают для защиты грунтов засыпки и предотвращения размывания. Было отмечено, что необходимы более глубокие исследования из-за отсутствия опыта в отношении проектирования, анализа (например, сопротивления вертикальным и боковым нагрузкам), испытаний под нагрузкой и процедуры строительства в недавнем отчете по проекту Департамента транспорта штата Айова (Эванс).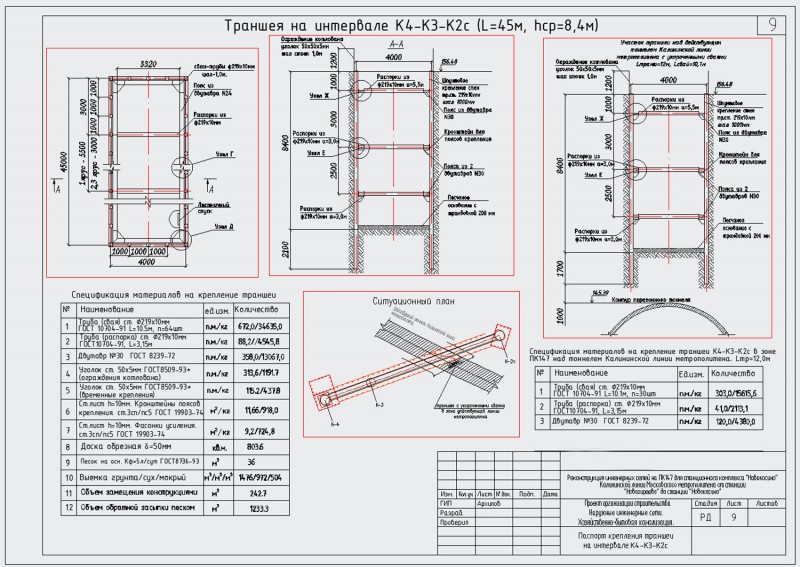 и др., 2012). Например, было отмечено, что в США нет специальной процедуры проектирования отчасти потому, что концепция шпунтовых свай с осевой нагрузкой является здесь относительно новой.Шпунтовые сваи анализируются как удерживающая грунт конструкция в большинстве методов проектирования, например, в Небраске, что означает, что боковое давление грунта будет контролировать подход к проектированию. Комбинированное воздействие осевой и поперечной нагрузки необходимо учитывать, когда в проекте предполагается осевая система устоя шпунтовой сваи.
и др., 2012). Например, было отмечено, что в США нет специальной процедуры проектирования отчасти потому, что концепция шпунтовых свай с осевой нагрузкой является здесь относительно новой.Шпунтовые сваи анализируются как удерживающая грунт конструкция в большинстве методов проектирования, например, в Небраске, что означает, что боковое давление грунта будет контролировать подход к проектированию. Комбинированное воздействие осевой и поперечной нагрузки необходимо учитывать, когда в проекте предполагается осевая система устоя шпунтовой сваи.
Язык
Проект
Тема/Указатель Термины
Информация о подаче
- Регистрационный номер: 01769367
- Тип записи: Исследовательский проект
- Агентство-источник: Департамент транспорта штата Небраска
- Файлы: RIP, STATEDOT
- Дата создания: 12 апр 2021 14:29
Метод расчета водоизмещения передней стенки крытого шпунтового причала
Крытые шпунтовые причалы широко используются в портовом, водном и гражданском строительстве. Эта статья основана на теории давления грунта и эффекте выгиба грунта. По напряженно-деформационным характеристикам крытого шпунтового причала выведены формулы для расчета усилия и деформации передней стенки крытого шпунтового причала при статических нагрузках. Точность теоретического расчета проверяется путем сравнения фактических измеренных данных о напряжении и деформации порта Jingtang 32#. Сравнение показывает, что при расчете смещения разреза ниже границы поверхности бурового раствора результаты согласуются с натурными данными.Однако при расчете смещения участка над границей поверхности бурового раствора, если смещение точки крепления не учитывать, поскольку смещение точки крепления ограничено искусственно, расчетное натяжение анкерной тяги будет относительно большим. Это приводит к значительному снижению результата расчета разреза над границей поверхности бурового раствора, который сильно отличается от реальных результатов натурных измерений. Если учитывать смещение точки крепления, расчетное натяжение анкерной тяги является более точным, а результаты расчета смещения передней стенки очень близки к результатам измерений на месте, поскольку смещение точки крепления принимается научно.
Эта статья основана на теории давления грунта и эффекте выгиба грунта. По напряженно-деформационным характеристикам крытого шпунтового причала выведены формулы для расчета усилия и деформации передней стенки крытого шпунтового причала при статических нагрузках. Точность теоретического расчета проверяется путем сравнения фактических измеренных данных о напряжении и деформации порта Jingtang 32#. Сравнение показывает, что при расчете смещения разреза ниже границы поверхности бурового раствора результаты согласуются с натурными данными.Однако при расчете смещения участка над границей поверхности бурового раствора, если смещение точки крепления не учитывать, поскольку смещение точки крепления ограничено искусственно, расчетное натяжение анкерной тяги будет относительно большим. Это приводит к значительному снижению результата расчета разреза над границей поверхности бурового раствора, который сильно отличается от реальных результатов натурных измерений. Если учитывать смещение точки крепления, расчетное натяжение анкерной тяги является более точным, а результаты расчета смещения передней стенки очень близки к результатам измерений на месте, поскольку смещение точки крепления принимается научно.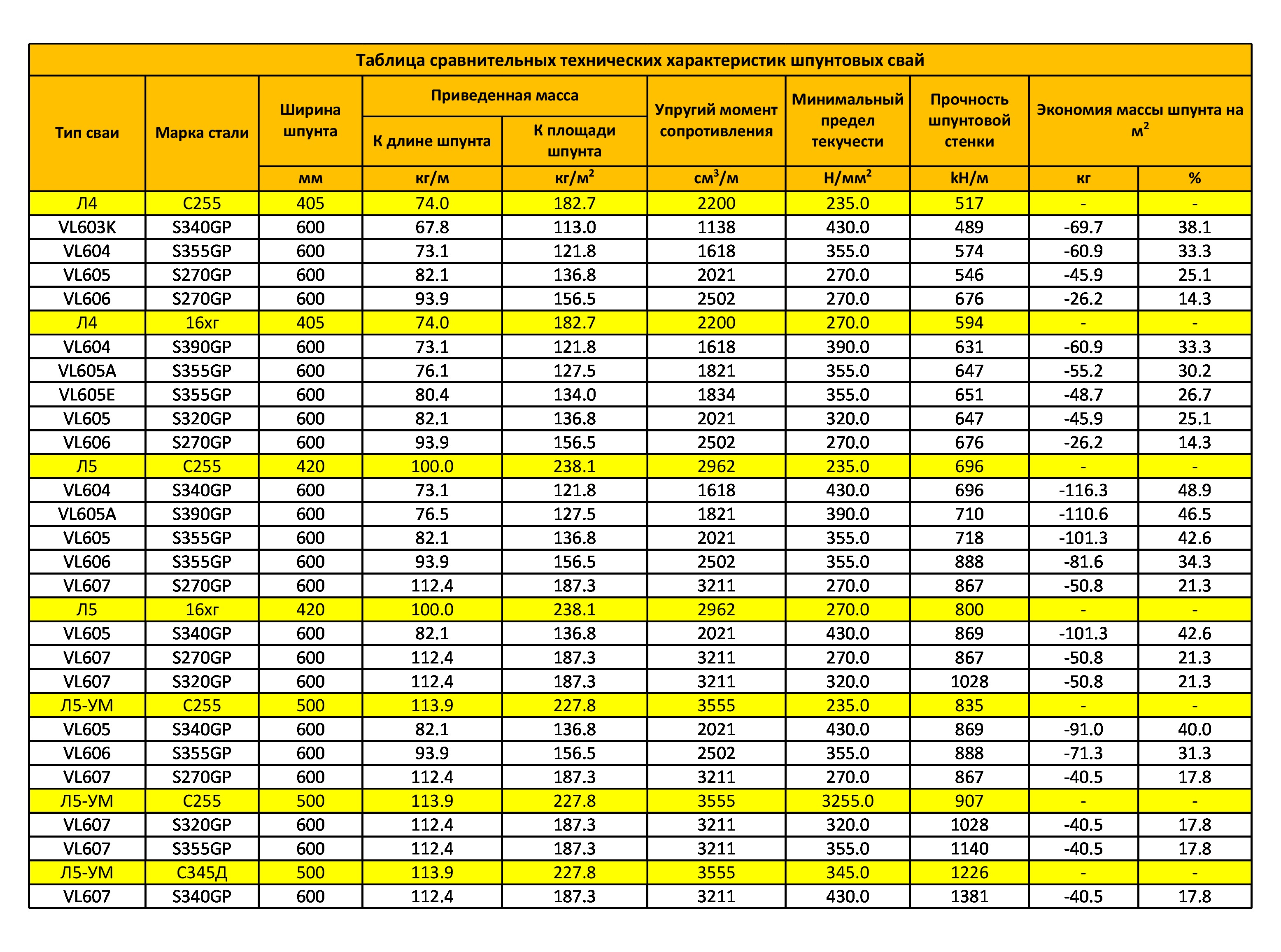
1. Введение
Для разработки шпунтовых причалов для глубоководных и больших причалов Первый исследовательский и проектный институт железных дорог Китая в течение многих лет проектировал и исследовал причалы, в 2002 году предложил новый тип крытых шпунтовых причалов и успешно построен глубоководный причальный причал грузоподъемностью 100 тыс. тонн [1].
Шпунтовые причальные конструкции включают передние шпунтовые стены, скрытые сваи, анкерные стены, анкерные стержни и причальное оборудование. Конструкция шпунтовой пристани показана на рисунке 1.Он характеризуется добавлением ряда железобетонных монолитных свай [2], представляющих собой засыпные сваи, между фасадными и анкерными стенками. Расстояние между фасадными шпунтовыми стенами 3∼5 м. Обычно засыпные сваи располагают с промежутками. Передние шпунтовые стены, засыпные сваи и анкерные стены соединяются в единую конструкцию передними и задними стяжками. Наличие закрытых свай противостоит давлению грунта за стеной и снижает давление грунта, действующее непосредственно на передние шпунтовые стенки. Соответствующие исследования показали, что при нормальных расчетных условиях закрытые сваи уменьшают положительный и отрицательный изгибающие моменты фасадных стен примерно на 70 % и 10 % соответственно и не оказывают большого влияния на усилия анкерной стены [3]. Применение и разработка нового типа крытого шпунтового причала обеспечивает техническую возможность создания шпунтовых причалов для глубоководья [4]. Исследователи приложили большие усилия для исследования сейсмического анализа заанкерованных шпунтовых стенок причалов [6–8].Несколько теорий и результатов по сейсмическому анализу шпунтовых причалов были разработаны за последние несколько десятилетий посредством экспериментов с испытаниями на вибростенде [6, 8, 9–11]. Предложено фундаментальное исследование по простому методу оценки сейсмических характеристик шпунтовых причальных стенок с вертикальной анкеровкой свай против подвижек грунта при землетрясении первого уровня [12]. Исследовано явление большой деформации шпунтовой причальной стенки и разрушения свайного фундамента из-за бокового растекания, вызванного разжижением, в районе порта [13–15].
Соответствующие исследования показали, что при нормальных расчетных условиях закрытые сваи уменьшают положительный и отрицательный изгибающие моменты фасадных стен примерно на 70 % и 10 % соответственно и не оказывают большого влияния на усилия анкерной стены [3]. Применение и разработка нового типа крытого шпунтового причала обеспечивает техническую возможность создания шпунтовых причалов для глубоководья [4]. Исследователи приложили большие усилия для исследования сейсмического анализа заанкерованных шпунтовых стенок причалов [6–8].Несколько теорий и результатов по сейсмическому анализу шпунтовых причалов были разработаны за последние несколько десятилетий посредством экспериментов с испытаниями на вибростенде [6, 8, 9–11]. Предложено фундаментальное исследование по простому методу оценки сейсмических характеристик шпунтовых причальных стенок с вертикальной анкеровкой свай против подвижек грунта при землетрясении первого уровня [12]. Исследовано явление большой деформации шпунтовой причальной стенки и разрушения свайного фундамента из-за бокового растекания, вызванного разжижением, в районе порта [13–15]. Оптимизационная модель для прогнозирования бокового смещения, вызванного разжижением, была создана Калантари [16]. Для групп свай за причальными стенками, подверженных боковому течению разжиженного грунта, могут быть приняты смягчающие меры [17]. Можно вывести передаточную формулу для горизонтальной тяги, действующей на плоскость шпунта с покрытием на суше [17, 18]. К сожалению, в настоящее время исследования крытых шпунтовых конструкций причалов носят поверхностный характер. На сегодняшний день не существует систематических, обоснованных, практичных теорий методов расчета.Поэтому исследования крытых шпунтовых причальных сооружений имеют большое практическое значение.
Оптимизационная модель для прогнозирования бокового смещения, вызванного разжижением, была создана Калантари [16]. Для групп свай за причальными стенками, подверженных боковому течению разжиженного грунта, могут быть приняты смягчающие меры [17]. Можно вывести передаточную формулу для горизонтальной тяги, действующей на плоскость шпунта с покрытием на суше [17, 18]. К сожалению, в настоящее время исследования крытых шпунтовых конструкций причалов носят поверхностный характер. На сегодняшний день не существует систематических, обоснованных, практичных теорий методов расчета.Поэтому исследования крытых шпунтовых причальных сооружений имеют большое практическое значение.
В этой статье расчет смещения передней стенки был произведен теоретически на основе гипотезы Винклера. Формулы давления грунта и перемещений фасадных шпунтовых стен в глубинной части грунта рассчитываются методом «m» при статических нагрузках. Передние шпунтовые стены в шпунтовых причалах рассчитывались по теории активного давления грунта. Теория эффекта сводообразования грунта была объединена со значениями коэффициента бокового давления грунта параллельной стены докторантом Цзяном [19], и было рассчитано напряжение на передних стенах крытых шпунтовых причалов.На основе уравнения кривой прогиба и деформационных характеристик механики материалов получены формулы перемещений для деформации передних стенок шпунтовой пристани под действием статической нагрузки.
Теория эффекта сводообразования грунта была объединена со значениями коэффициента бокового давления грунта параллельной стены докторантом Цзяном [19], и было рассчитано напряжение на передних стенах крытых шпунтовых причалов.На основе уравнения кривой прогиба и деформационных характеристик механики материалов получены формулы перемещений для деформации передних стенок шпунтовой пристани под действием статической нагрузки.
Наконец, с использованием относительно зрелой теории статического давления грунта и теории эффекта сводообразования грунта, формулы смещения передней стены крытого шпунтового причала под действием статической нагрузки выводятся и сравниваются с данными наблюдений на месте в порту Цзинтан 10. # причал пристань и пристань Jingtang Port 32 # для проверки точности теоретического вывода.
2. Предположение Винклера
В методе реакции упругого основания, основанном на предположении Винклера, при расчете сваи предполагается, что сила реакции грунта пропорциональна n -й степени смещения сваи , то есть,где боковой прогиб точка расчета сваи (м), глубина точки расчета сваи (м), коэффициент грунта.
Мэтлок и Рис [20] отметили, что коэффициент заземления должен быть как можно более простым, и предложили два вида соотношений, а именно: считается, что коэффициент фундамента изменяется по степенному закону с глубиной, соответствующей фактической глубине, то есть где пропорциональный коэффициент, в то время как коэффициент фундамента меняется с глубиной, это чистые значения, которые меняются в зависимости от типа породы [21–24]. ], и является константой, относящейся к категории скального грунта.Значения должны быть определены экспериментально. В соответствии с различными значениями закон изменения коэффициента фундамента с глубиной в уравнении (1) может быть представлен, как показано на рисунке 2.
3. Расчет перемещений передней стены
3.1. Упрощенная расчетная модель и распределение площади давления на грунт крытой шпунтовой конструкции причала
Расчетная модель крытой шпунтовой пристани состоит из передних шпунтовых стен, покрытых свай, анкерных стен, а также передних и задних анкерных стержней, как показано на Рисунок 3.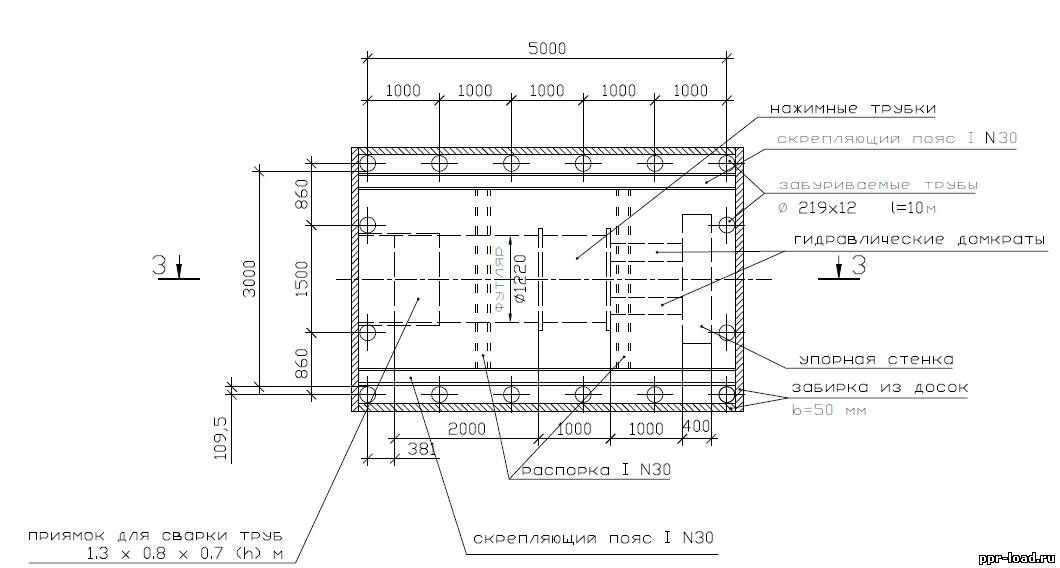 При расчете давления грунта грунты предполагаются находящимися в предельном равновесии, при этом влияние волновой силы не учитывается.
При расчете давления грунта грунты предполагаются находящимися в предельном равновесии, при этом влияние волновой силы не учитывается.
Самая большая разница между крытой шпунтовой пристанью и традиционной шпунтовой пристанью заключается в том, что крытые сваи устанавливаются между передними стенами и анкерными стенками, а крытые сваи сопротивляются грунту за сваями и уменьшают землю нагрузка непосредственно на передние стенки. Чтобы детально проанализировать влияние закрытых свай, грунты разделены на пять областей, которые будут обсуждаться отдельно.Участки 1 и 4 – лицевая шпунтовая стенка и засыпная свая соответственно, находящиеся в грунте. Поскольку горизонтальное смещение конструкции под действием статических нагрузок относительно невелико, для расчета горизонтального давления грунта используется метод упругого сопротивления, а коэффициент горизонтального сопротивления зависит от метода «m». Давление грунта в зонах 2 и 3 более сложное. Грунты на этих участках находятся между фасадными шпунтовыми стенками и засыпными сваями.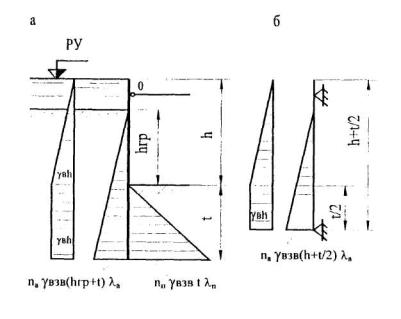 Относительное смещение между передними шпунтовыми стенками и засыпными сваями оказывает важное влияние на величину давления грунта.В практическом инженерном проектировании жесткость скрытой сваи часто рассчитывается большей, чтобы уменьшить давление грунта на переднюю стенку. В результате смещение передней стенки больше, чем смещение закрытой сваи. Грунты между фасадными стенами и засыпными сваями имеют тенденцию к смещению в сторону моря, а давление грунта находится в парциальном активном состоянии. Следовательно, коэффициенты давления грунта в зонах 2 и 3 должны быть между активным давлением грунта и стационарным давлением грунта. В этой статье Цзян Бо, докторант Университета Чжэцзян, пришел к выводу, что следует использовать коэффициенты бокового давления грунтов с параллельными стенками.Рекомендуемые коэффициенты боковых давлений показаны в таблице 1.
Относительное смещение между передними шпунтовыми стенками и засыпными сваями оказывает важное влияние на величину давления грунта.В практическом инженерном проектировании жесткость скрытой сваи часто рассчитывается большей, чтобы уменьшить давление грунта на переднюю стенку. В результате смещение передней стенки больше, чем смещение закрытой сваи. Грунты между фасадными стенами и засыпными сваями имеют тенденцию к смещению в сторону моря, а давление грунта находится в парциальном активном состоянии. Следовательно, коэффициенты давления грунта в зонах 2 и 3 должны быть между активным давлением грунта и стационарным давлением грунта. В этой статье Цзян Бо, докторант Университета Чжэцзян, пришел к выводу, что следует использовать коэффициенты бокового давления грунтов с параллельными стенками.Рекомендуемые коэффициенты боковых давлений показаны в таблице 1.
+ + + 27 ° + + + 0,306
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.2. Расчет давления грунта между передними шпунтовыми стенами и засыпными сваями
Боковое давление грунта между передними шпунтовыми стенами и засыпными сваями обычно рассчитывается с использованием теории параллельных стен.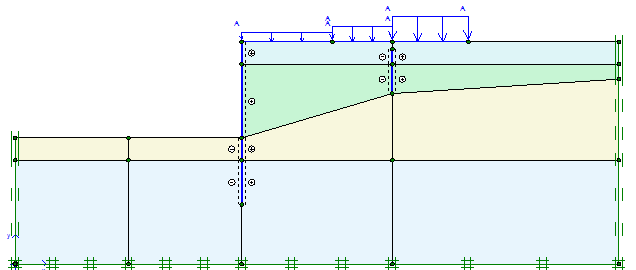 При расчете единичная ширина стены принимается по ширине передней шпунтовой стены в горизонтальном направлении. Расстояние между стяжками также может быть выбрано в качестве расчетной единицы. В вертикальном направлении микроячейка забирается вглубь вдоль стены. Затем проводятся силовые анализы микроэлемента. Вертикальное напряжение можно получить, используя интеграл уравнения равновесия. Боковое давление грунта на любой глубине передней шпунтовой стенки можно получить, умножив вертикальное напряжение на коэффициент бокового давления [25].
При расчете единичная ширина стены принимается по ширине передней шпунтовой стены в горизонтальном направлении. Расстояние между стяжками также может быть выбрано в качестве расчетной единицы. В вертикальном направлении микроячейка забирается вглубь вдоль стены. Затем проводятся силовые анализы микроэлемента. Вертикальное напряжение можно получить, используя интеграл уравнения равновесия. Боковое давление грунта на любой глубине передней шпунтовой стенки можно получить, умножив вертикальное напряжение на коэффициент бокового давления [25].
В соответствии с теорией параллельных стен вдоль длины поперечного сечения параллельной стены на любой глубине толщина B используется в микрогрунте, как показано на рис. 4. Единичная ширина рассчитывается для анализа сил микрогрунта:( 1)Вес грунта, :(2)Верхнее и нижнее поверхностное давление микрогрунта: Вертикальное давление верхней поверхности: Вертикальное давление нижней поверхности:(3)Трение вблизи микрогрунта:где угол трения грунтов у передних стенок шпунта .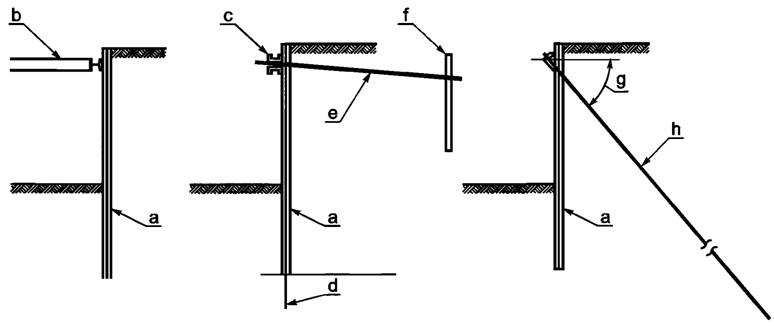 Угол трения может быть выбран в зависимости от шероховатости и условий дренажа: (1) Гладкая и плохо дренируемая, (2) Шероховатая и хорошо дренируемая, (3) Очень шероховатая и хорошо дренируемая,
Угол трения может быть выбран в зависимости от шероховатости и условий дренажа: (1) Гладкая и плохо дренируемая, (2) Шероховатая и хорошо дренируемая, (3) Очень шероховатая и хорошо дренируемая,
Приведенное выше уравнение равновесия может быть получено согласно к вертикальному балансу сил микроэлементов:
Граничное условие:
С учетом уравнения (12),
Приведенные формулы не учитывают сил сцепления глинистых грунтов.Поэтому, когда грунт представляет собой глину, следует учитывать внутренние силы, создаваемые силой сцепления. Внутреннюю силу, создаваемую силой сцепления, приблизительно принимают за равномерную силу на граничных поверхностях грунтов, подставив ее в уравнение (13), можно получить расчетную формулу для глинистых грунтов:
3.3. Расчет усилий передних стен, передаваемых от грунтов между засыпными сваями
Согласно результатам предыдущих исследований, грунтовый свод между сваями можно разделить на две части, как показано на рисунке 5.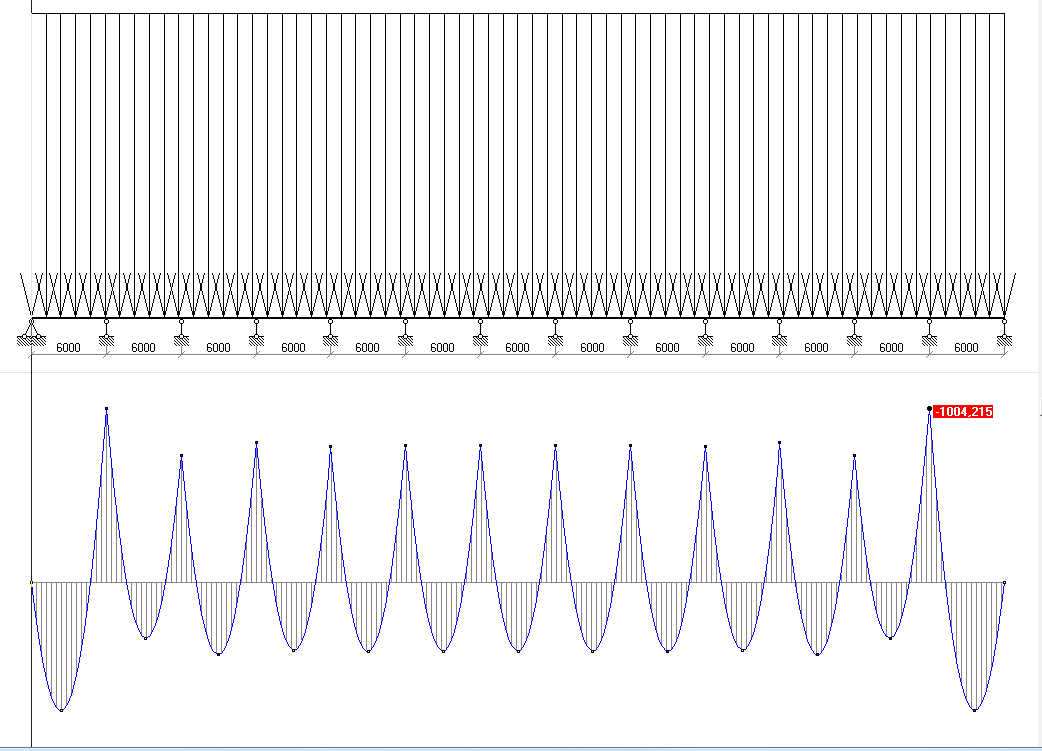
Предполагается, что давление грунта вдали передается на соседние закрытые сваи через наружную арочную зону и устойчивую внутреннюю арочную зону, а передние шпунтовые стены могут использоваться как пара параллельных стен. Когда линия давления арки совпадает с осью арки, изгибающий момент каждой секции равен нулю, арки не имеют изгибающего момента и стоимость материала наиболее экономична. Поскольку трехшарнирная арочная конструкция и нагрузки симметричны, в качестве объекта исследования рассматривается половина трехшарнирной арки.Система координат настроена, как показано на рисунке 6. Уравнение для разумной оси арки:
Сила реакции основания арки:
В сочетании с уравнением для разумной оси арки рассчитывается по формуле, где l равно пролет арки, высота арки, угол трения.
Вдоль вертикального направления на любой глубине берется микрогрунт толщиной , как показано на рисунке 7. Силы, действующие на микрогрунт в вертикальном направлении, следующие:
Сила тяжести:где .
Трение между грунтами и передними стенками шпунтовых свай:
Трение грунта на грунтовых сводах:
Разность давлений грунта между верхней и нижней поверхностями:
Уравнение равновесия микрогрунтов по вертикальным силам: где и — вертикальное напряжение и горизонтальное стресс соответственно.
Силы, передаваемые от грунтов в арках на передние шпунтовые стены, предполагаются равномерно распределенными в горизонтальной плоскости. Силы распределяются в вертикальном направлении в соответствии с коэффициентом бокового давления .В сочетании с приведенными выше формулами получается следующая формула:
Согласно аналитической теории дифференциальных уравнений можно получить следующую формулу:
Граничное условие:
Подставляя уравнение (25) в уравнение (24), получаем следующее получается формула:
Приведенные выше формулы не учитывают силы сцепления глинистых грунтов. Поэтому, когда грунт представляет собой глину, следует учитывать внутренние силы, создаваемые силой сцепления. Внутреннее усилие, создаваемое силой сцепления, считается примерно равномерным усилием на граничных поверхностях грунтов. Подставляя эту силу в уравнение (27), можно получить расчетную формулу для глинистых грунтов:
Внутреннее усилие, создаваемое силой сцепления, считается примерно равномерным усилием на граничных поверхностях грунтов. Подставляя эту силу в уравнение (27), можно получить расчетную формулу для глинистых грунтов:
Давление грунта на передние шпунтовые стены, приближенные к земле, вычисляют по формуле
3.4. Давление грунта на передние шпунтовые стенки под поверхностью ила
При расчете давления грунта на передние шпунтовые стенки, находящиеся ниже поверхности ила, с учетом жесткости шпунтовых причалов с покрытием при статических нагрузках большая, но горизонтальное смещение, создаваемое конструкцией, относительно невелико, и используется метод упругого сопротивления, то есть горизонтальное сопротивление грунта на любой глубине пропорционально горизонтальному смещению грунта, то есть
. В настоящее время используется метод «m» в портовом машиностроении Китая для определения коэффициента горизонтального сопротивления.Предполагая, что коэффициент сопротивления земли увеличивается линейно с глубиной,
Подставляя уравнение (31) в уравнение (30), вычисляется как
3.
 5. Давление грунта на передние шпунтовые стены над поверхностью грязи
5. Давление грунта на передние шпунтовые стены над поверхностью грязи Расчет смещения для передних шпунтовых стен крытых шпунтовых причалов такой же, как и для традиционных шпунтовых причалов. Поскольку напряжённые характеристики и механизм деформирования лобовых шпунтовых стенок, находящихся в грунтах, совершенно отличны от таковых над поверхностью ила, то передняя шпунтовая стенка разделяется на верхнюю и нижнюю части на поверхности ила для раздельных расчётов.Ниже поверхности ила стенки шпунтовых свай можно упростить как эластичные конструкции, заглубленные в грунт, с верхним слоем, совмещенным с поверхностью ила. Вершина сваи имеет момент и боковую силу. и являются равнодействующими момента и силы на поверхности грязи шпунтовой стенки от силы над поверхностью грязи шпунтовой стенки. Угол поворота и смещение вершины сваи равны и соответственно. Согласно предыдущему описанию, когда боковое смещение сваи происходит на глубине , сила сопротивления грунта, действующая на сваи на глубине, равнаДавление перегруженного грунта распределяется в среднем по ширине грунта между засыпными сваями и за засыпными сваями и имеет величину, которая рассчитывается по формуле где горизонтальное давление грунта, создаваемое грунтами между засыпными сваями и передними шпунтовыми стенками на поверхности бурового раствора, и – сила сцепления (кПа) и угол внутреннего трения на поверхности бурового раствора соответственно.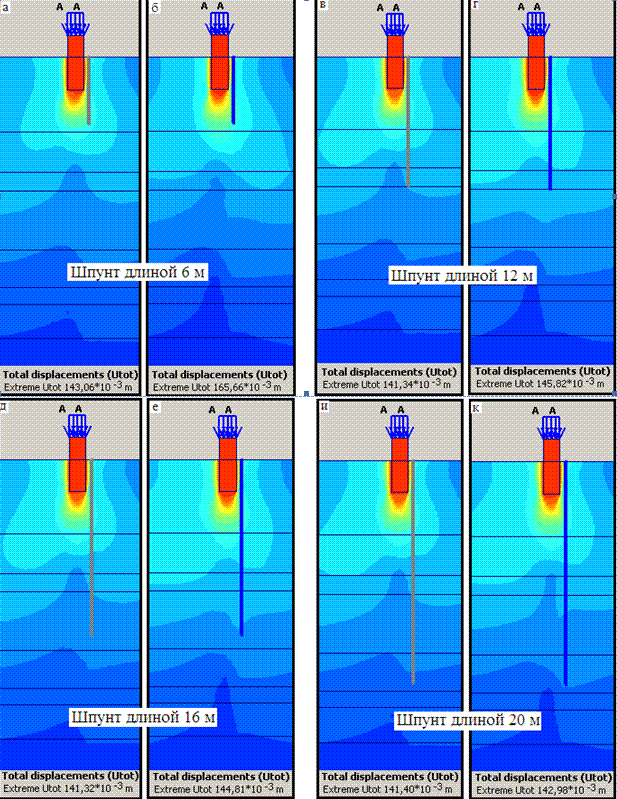
Учитывая глубину преобразования , на основании дифференциального уравнения кривой прогиба в механике материалов получаются следующие формулы:
Подставляя уравнение (33) в уравнение (35),
Граничные условия: дифференциальных уравнений, решение уравнения (36) может быть выражено следующим степенным рядом:
Выводом может быть получена следующая формула:
В сочетании с донными граничными условиями: поверхности рассчитываются отдельно как
Перерезывающую силу и изгибающий момент передних шпунтовых стенок на поверхности ила следует рассчитывать суммарно: где – расстояние от подошвы слоя до поверхности причала (м), – расстояние от точка давления грунта пласта на переднюю поверхность бурового раствора (м).
3.6. Расчет смещения передней стены, когда смещение точки крепления игнорируется
Динамическая водяная нагрузка является переменным параметром, который также полезен для уменьшения смещения причала шпунтовой сваи передней стены. Поэтому в статье выведена методика расчета перемещений на передней стенке с учетом наиболее опасной ситуации без динамической гидронагрузки.
Поэтому в статье выведена методика расчета перемещений на передней стенке с учетом наиболее опасной ситуации без динамической гидронагрузки.
При достаточной прочности свайной или анкерной конструкции смещение верхней части передних шпунтовых стенок меньше, смещения в средней и нижней части больше, передние шпунтовые стенки имеют тенденцию к повороту вокруг точка крепления, а смещение в точке крепления незначительно по сравнению с перемещением дна.Предполагается, что смещение в точке крепления равно нулю, когда вычисляются натяжение тяги и смещение передней стенки, и процесс решения выглядит следующим образом.
Смещение передней шпунтовой стенки в точке крепления в основном состоит из четырех частей: смещение на поверхности бурового раствора, смещение, вызванное вращением на поверхности бурового раствора, смещение передней шпунтовой стенки в точке крепления, вызванное грунтом давление за стеной и смещение передней шпунтовой стенки в точке крепления, вызванное натяжением анкерной тяги.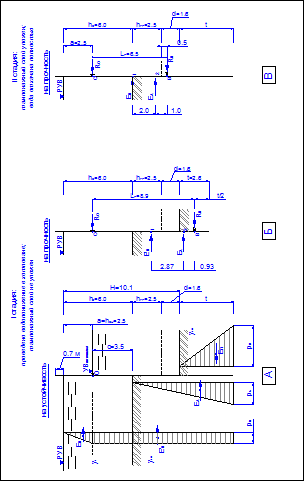 Смещение передней шпунтовой стенки в точке крепления принимается равным нулю. Получается следующая формула:(1)Рассчитать смещение .
Смещение передней шпунтовой стенки в точке крепления принимается равным нулю. Получается следующая формула:(1)Рассчитать смещение .
Согласно формуле механики материалов:
Граничные условия:
В сочетании с граничными условиями решение формулы выражается как
Преобразование уравнения (49) в формулу с глубиной в качестве переменной, формула выражается как
Смещение выражается формулой (2)Рассчитать смещение .
Согласно формуле механики материалов:
Граничные условия:
Таким образом, смещения и выражаются как
Смещения в любой точке передней шпунтовой стенки над поверхностью бурового раствора могут быть выражены как
Наконец, формулы для расчета смещения любой точки передней шпунтовой стенки над поверхностью бурового раствора могут быть выражены как
3.7. Учет смещения точки крепления для расчета смещения передней стены
При недостаточной прочности засыпной сваи или анкерной конструкции смещения верхней части передних шпунтовых стенок больше, смещения в нижней части меньше, передней шпунтовые стенки имеют тенденцию к вращению вокруг нижней части передней шпунтовой стенки, и смещение в точке крепления не является незначительным. Предполагается, что смещение в точке крепления имеет определенное значение при расчете натяжения анкерной тяги и смещения передней стенки, и процесс решения выглядит следующим образом.
Предполагается, что смещение в точке крепления имеет определенное значение при расчете натяжения анкерной тяги и смещения передней стенки, и процесс решения выглядит следующим образом.
Перемещение в точке крепления . Подставляя это в уравнение (57), получаем следующее уравнение:
Для определения рекомендуется следующая формула:
Смещение в любой точке передних шпунтовых стенок над поверхностью бурового раствора можно выразить как смещение в любой точке над поверхностью раствора передних шпунтовых стенок можно выразить как
3.8. Блок-схема расчета смещения передней стенки
Блок-схема процесса расчета смещения передней стенки крытых шпунтовых причалов под действием статических нагрузок представлена на рисунке 8.
4. Пример расчета смещения передней Стена крытого шпунтового причала
4.1. Обзор проекта
Модель расчета основана на причале порта Цзинтан 32#. Передние стены и конструкция анкерной стены представляют собой непрерывные подземные стены. Расстояние между покрытыми сваями 1,2 м, форма поперечного сечения показана на рис. 9. Параметры грунта, стены и анкерных стержней приведены в табл. 2. Материал Тип Единира Вес (KN / M 3 ) Угол внутреннего трения (°) Сплоченность (KPA) Упругостиящая модуль (MPA) Соотношение Poisson слой 1 18.0 32.0 32.0 5 26.00 0.29 18.0 18.0 28.0 5 26.00 0.29 почвенный слой 3 19.1 27,0 20 8.97 0.30 0.30 Point Player 4 19.0 28.0 16 16 12.60 0.30 Почвенный слой 5 17.6 17.1 16 3.
Расстояние между покрытыми сваями 1,2 м, форма поперечного сечения показана на рис. 9. Параметры грунта, стены и анкерных стержней приведены в табл. 2. Материал Тип Единира Вес (KN / M 3 ) Угол внутреннего трения (°) Сплоченность (KPA) Упругостиящая модуль (MPA) Соотношение Poisson слой 1 18.0 32.0 32.0 5 26.00 0.29 18.0 18.0 28.0 5 26.00 0.29 почвенный слой 3 19.1 27,0 20 8.97 0.30 0.30 Point Player 4 19.0 28.0 16 16 12.60 0.30 Почвенный слой 5 17.6 17.1 16 3. 60 0.30 1 897 0.30 почвенный слой 7 19.7 31.0 5 26.00 26.00 0.29 Почвенный слой 8 19.7 19.7 31 31 8.97 0.30 Уровень почвы 9 19.7 32.0 5.0 5 26.00 0.29 бетона 25.0 — — — 2,82070
60 0.30 1 897 0.30 почвенный слой 7 19.7 31.0 5 26.00 26.00 0.29 Почвенный слой 8 19.7 19.7 31 31 8.97 0.30 Уровень почвы 9 19.7 32.0 5.0 5 26.00 0.29 бетона 25.0 — — — 2,82070
Нанкин Гидравлический научно-исследовательский институт организовал соответствующий персонал для завершения установки приборостроения в феврале 2005 года, а также период наблюдения был с июня 2005 года по февраль 2008 года. Результаты наблюдений приведены в таблице 3.
Результаты наблюдений приведены в таблице 3.
# 4
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.2. Результаты теоретических расчетов
В соответствии с теорией расчета перемещений передней стенки крытого шпунтового причала под действием статических нагрузок, смещения передней стенки при пренебрежении или учете перемещений в точке крепления показаны в таблице 4.
0,255 -45,025 -154,785 -538,322 -0.016669 151,878 -0,0172 -0,00782 + -0,00491 + -0,0016787 y = -1.002 × 10 -6 Z 4 + 1.0106 × 10 -4 Z 3 + 0.222 Z — 5.630 × 10 -3 Z 2 + 4.587 × E -0.049 Z — 4.576
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.3. Сравнение и анализ результатов расчетов
Теоретический расчет и результаты натурных измерений смещения передней шпунтовой стенки крытого шпунтового причала показаны на рис. Учет или пренебрежение анкерной точкой мало влияет на расчет перемещений передней шпунтовой стенки, находящейся ниже поверхности бурового раствора.Результаты, полученные с использованием двух методов расчета, близки к измеренным данным. Результаты двух методов расчета сильно различаются при расчете смещения передней шпунтовой стенки, находящейся ниже поверхности бурового раствора. Когда смещение в точке крепления игнорируется, смещение в точке крепления ограничивается искусственно; следовательно, результат расчета натяжения стяжной тяги относительно велик, что приводит к значительному сокращению расчета смещения передней стенки над поверхностью бурового раствора.Форма деформации передней шпунтовой стенки представляет собой средневыпуклый барабан, а максимальное смещение составляет примерно 20 мм, что сильно отличается от реальных результатов измерений на месте.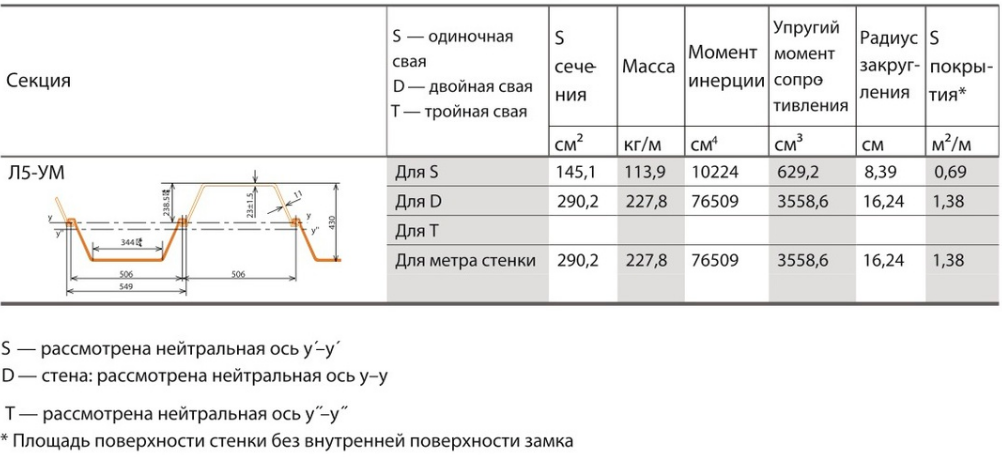
При рассмотрении смещения в точке крепления расчетное натяжение анкерной тяги является более точным, а расчет смещения передней стенки очень близок к результату измерения на месте, поскольку смещение точки крепления принимается научно. Верхняя часть передней стенки частично защемлена в режиме наклонного деформирования.Максимальное смещение в точке крепления передней стенки составляет примерно 55 мм, измеренное максимальное смещение составляет примерно 60 мм, а погрешность составляет 8,33%, что является идеальным. В заключение, более научно использовать гипотетическое смещение точки крепления, предложенное в этой статье.
5. Заключение
Эта статья основана на теории давления грунта и эффекте выгиба грунта. По напряженно-деформационным характеристикам крытого шпунтового причала выводятся формулы, используемые для расчета усилия и деформации передней стенки крытого шпунтового причала при статических нагрузках, и сравнение фактически измеренных напряжений и деформаций данные порта Jingtang 32 # используются для проверки точности теоретического вывода./87e499ae47fe1a2.s.siteapi.org/img/228338cf2e30666a06d59f67b7265203927507d2.png) Сравнение показывает, что при расчете смещения передней шпунтовой стенки, находящейся ниже поверхности бурового раствора, результаты двух методов не сильно различаются и хорошо согласуются с данными полевых измерений. Однако при расчете смещения лобового шпунтового борта, находящегося над поверхностью раствора, и пренебрежении смещениями в анкерной точке смещения в анкерной точке ограничиваются искусственно. Следовательно, результат натяжения анкера относительно велик, что приводит к значительному уменьшению расчетного смещения передней шпунтовой стенки, находящейся над поверхностью бурового раствора.Форма деформации передней шпунтовой стенки представляет собой средний выпуклый барабан, а максимальное смещение составляет примерно 20 мм, что сильно отличается от фактических результатов измерений на месте. Когда учитывается смещение в точке крепления, расчетное натяжение анкерной тяги является более точным, а результаты смещения передней стенки очень близки к результатам измерений на месте, поскольку смещение в точке крепления предполагается научно.
Сравнение показывает, что при расчете смещения передней шпунтовой стенки, находящейся ниже поверхности бурового раствора, результаты двух методов не сильно различаются и хорошо согласуются с данными полевых измерений. Однако при расчете смещения лобового шпунтового борта, находящегося над поверхностью раствора, и пренебрежении смещениями в анкерной точке смещения в анкерной точке ограничиваются искусственно. Следовательно, результат натяжения анкера относительно велик, что приводит к значительному уменьшению расчетного смещения передней шпунтовой стенки, находящейся над поверхностью бурового раствора.Форма деформации передней шпунтовой стенки представляет собой средний выпуклый барабан, а максимальное смещение составляет примерно 20 мм, что сильно отличается от фактических результатов измерений на месте. Когда учитывается смещение в точке крепления, расчетное натяжение анкерной тяги является более точным, а результаты смещения передней стенки очень близки к результатам измерений на месте, поскольку смещение в точке крепления предполагается научно. Верхняя часть передней стенки частично защемлена в режиме наклонного деформирования.Максимальное смещение в точке крепления передней стенки составляет примерно 55 мм, измеренное максимальное смещение составляет примерно 60 мм, а погрешность составляет 8,33%, что является идеальным. В заключение, более научно использовать гипотетическое смещение точки крепления, предложенное в этой статье.
Верхняя часть передней стенки частично защемлена в режиме наклонного деформирования.Максимальное смещение в точке крепления передней стенки составляет примерно 55 мм, измеренное максимальное смещение составляет примерно 60 мм, а погрешность составляет 8,33%, что является идеальным. В заключение, более научно использовать гипотетическое смещение точки крепления, предложенное в этой статье.
Доступность данных
Данные, использованные для поддержки результатов этого исследования, можно получить у соответствующего автора по запросу.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в связи с публикацией данной статьи.
Благодарности
Это исследование было проведено при финансовой поддержке Фонда естественных наук провинции Цзянсу (грант № BK20161360), Six Major Talents Peak в провинции Цзянсу в Китае (грант № 2016-JZ-020), а также последипломного исследования и практики. Инновационная программа провинции Цзянсу (грант № SJCX17_0609).
(PDF) Метод расчета смещения на передней стене крытого шпунтового причала
шпунтовая стена, которая находится над поверхностью ила, значительно уменьшена
.Форма деформирования передней шпунтовой стенки
– средневыпуклый барабан, а максимальное смещение
примерно 20 мм, что сильно отличается от фактических результатов натурных измерений
. При смещении
в точке крепления расчетное натяжение анкерной тяги
является более точным, а результаты смещения передней стенки
очень близки к результатам измерений на месте
, поскольку предполагается смещение в точке крепления
научно. верхняя часть передней стенки частично
защемлена в режиме наклонного деформирования. Максимальное смещение
в точке крепления передней стенки составляет
примерно 55 мм, измеренное максимальное смещение
составляет примерно 60 мм, а погрешность составляет 8,33%, что
является идеальным. В заключение, более научно использовать hy-
смещение точки потенциальной опоры, предложенное в этой статье
.
Доступность данных
Данные, использованные для поддержки результатов этого исследования, доступны по запросу у соответствующего автора.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов
в отношении публикации данной статьи.
Благодарности
это исследование было выполнено при финансовой поддержке Natural
Science Foundation провинции Цзянсу (грант №
BK20161360), Six Major Talents Peak в провинции Цзянсу в
Китае (грант № 2020-J ), а также программа последипломных исследований
и практической инновационной деятельности провинции Цзянсу (грант
№.SJCX17_0609).
Ссылки
[1] YX Liu и ZD Wu, «Рабочий механизм шпунтовой сваи
причала с барьерными сваями», Hydro-Scienceand Engineering,
vol. 2, pp. 8–12, 2006.
[2] WP Liu, YR Zheng, ZY Cai, and ZB Jiao, «Метод конечных элементов
для крытых шпунтовых причалов», китайский
Journal of Geotechnical Engineering, vol.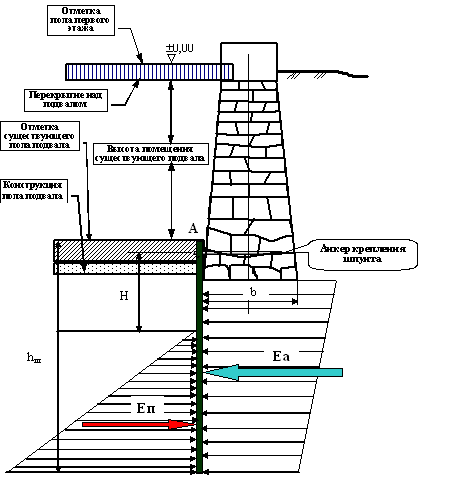 . 32, нет. 4, pp. 573–
. 32, нет. 4, pp. 573–
577, 2010.
[3] WC Dong, «Практика строительства глубоководных
свайно-стеновых причалов в порту Цзинтан и экспериментальное исследование», Port Engineering Технология, вып.12. С. 20–24. S1,
, стр. 30–32, 2005 г.
[5] LY Wang, HL Liu, PM Jiang, XX Chen, «Прогноз
метода сейсмической остаточной деформации стенки кессона
в жидком основании», China Ocean Engineering, vol. 25,
нет. 2011. Т. 1. С. 45–58.
[6] G. Gazetas, E.Гарини и А. Зафейракос, «Сейсмический анализ
высоких анкерных шпунтовых стен», Динамика грунта и землетрясение
Engineering, vol. 91, стр. 209–221, 2016.
[7] Дж. Леал, Дж. К. Де Ла Ллера и Г. Альдунейт, «Сейсмоизоляторы в причалах, опирающихся на сваи
», Труды портов, в Трудах
13th Triennial International, Сиэтл, Вашингтон, США, август
2013.
[8] А. Зекри, А. Галандарзаде, П. Гасеми и М. Хоссейн
Аминфар, «Экспериментальное исследование восстановительных мер
закреплено шпунтовых причальных стенок с использованием уплотнения грунта // Ocean
Engineering, vol.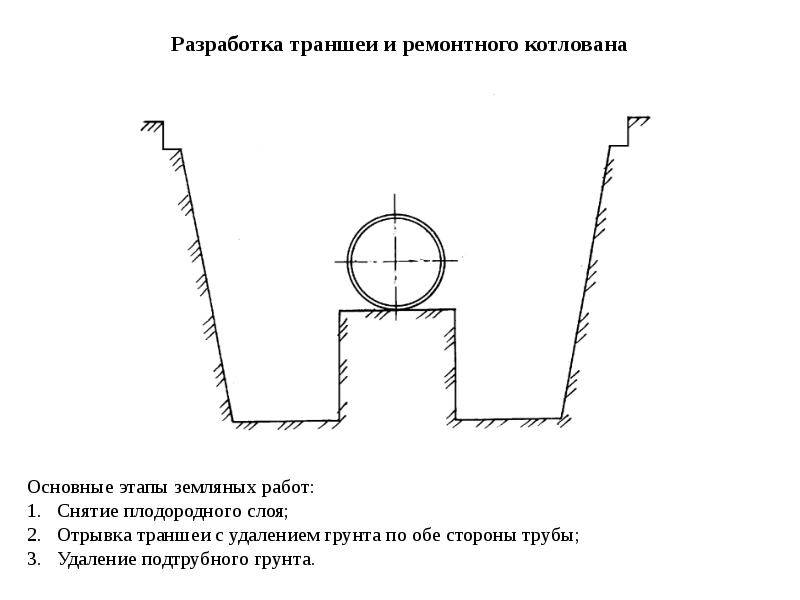 93, pp. 45–63, 2015.
93, pp. 45–63, 2015.
[9] C.W. Yu, C.J. Lee, W.Y. Hung, and H.-T. Чен, «Применение
преобразования Гильберта-Хуанга для характеристики разжижения грунта
и сейсмических откликов стенки причала, смоделированных в центрифужных
испытаниях с встряхивающим столом», Динамика грунта и проектирование землетрясений, том
,. 30, нет. 7, pp. 614–629, 2010.
[10] LY Wang, SK Chen, and P. Gao, «Исследование сейсмических
внутренних сил георешеток в армированных грунтовых подпорных стенах
конструкций в условиях землетрясений», Журнал виброинженерии
машиностроение, вып.16, нет. 4, pp. 2023–2034, 2014.
[11] LY Wang, GX Chen, and S. Chen, «Экспериментальное исследование сейсмической реакции
жестких подпорных стен, армированных георешеткой
, с насыщенным песком обратной засыпки», Geotextiles and Геомембраны,
т. 43, нет. 1, стр. 35–45, 2015.
[12] К. Мияшита и Т. Нагао, «Фундаментальное исследование простого метода оценки
сейсмических характеристик листовой
свайных причальных стенок с вертикальной анкеровкой свай против Первый уровень
землетрясение движения грунта», Журнал прикладной механики,
том. 10, pp. 601–611, 2007.
10, pp. 601–611, 2007.
[13] М. Сато и К. Табата, «Испытание на вибростенде крупногабаритной модели
механизма разрушения шпунтовой причальной стенки и свайного фундамента
из-за к боковому расширению», Японский геотехнический журнал
, том. 4, нет. 4, pp. 259–271, 2009.
[14] P. Ruggeri, D. Segato, and G. Scar-pelli, «Безопасность шпунтовых причальных стенок
: исследование отказов анкеров с предварительным натяжением»,
Журнал геотехнической и геоэкологической инженерии,
, том.9, нет. 139, pp. 1567–1574, 2013.
[15] BH Wang, ZH Wang, and X. Zuo, «Частотное уравнение
изгибной вибрирующей консольной балки с учетом вращательного
инерционного момента прикрепленной массы», Mathematical
Проблемы техники, вып. 2017, ID статьи 1568019,
5 страниц, 2017.
[16] Ф. Калантари, Х. МолаАбаси, М. Салахи и М. Вейскарами,
«Прогнозирование боковых смещений, вызванных разжижением
с использованием модели робастной оптимизации» , Scientia Iranica A, vol.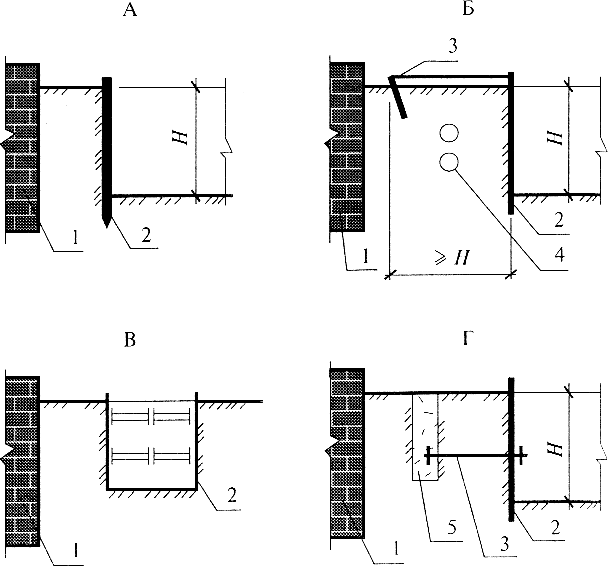 20,
20,
нет. 2, pp. 242–250, 2013.
[17] R. Motamed and I. Towhata, «Меры по смягчению последствий для групп свай
за стенками причала, подверженных боковому потоку разжиженного грунта
: модельные испытания вибростенда», Динамика грунтов и землетрясения
Инженерия, том. 10, нет. 30, pp. 1043–1060, 2010.
[18] LY Wang, GX Chen, P. Gao, and SK Chen, «Псевдостатический метод расчета сейсмической остаточной деформации армированной георешетки». грунтовая подпорная стенка с жидкой засыпкой // Виброинженерия.17, нет. 2,
, стр. 827–840, 2015 г.
[19] Б. Цзян, «Исследования эффекта выгиба грунта и давления грунта для подпорной конструкции
», докторская диссертация, Чжэцзянский университет,
, Ханчжоу, Китай, 2005 г.
[20] Х. Мэтлок и Л.С. Риз, «Обобщенные решения для свай с боковой нагрузкой», Журнал механики грунтов и фундаментов
Division, vol. 86, нет. СМ5, с. 63–91, 1960.
[21] Группа общего планирования 3-го проектного института
МПС, «Расчет фундамента опоры моста
с учетом упругого сопротивления грунта», Железная дорога
Информационный бюллетень по стандартному дизайну, №.

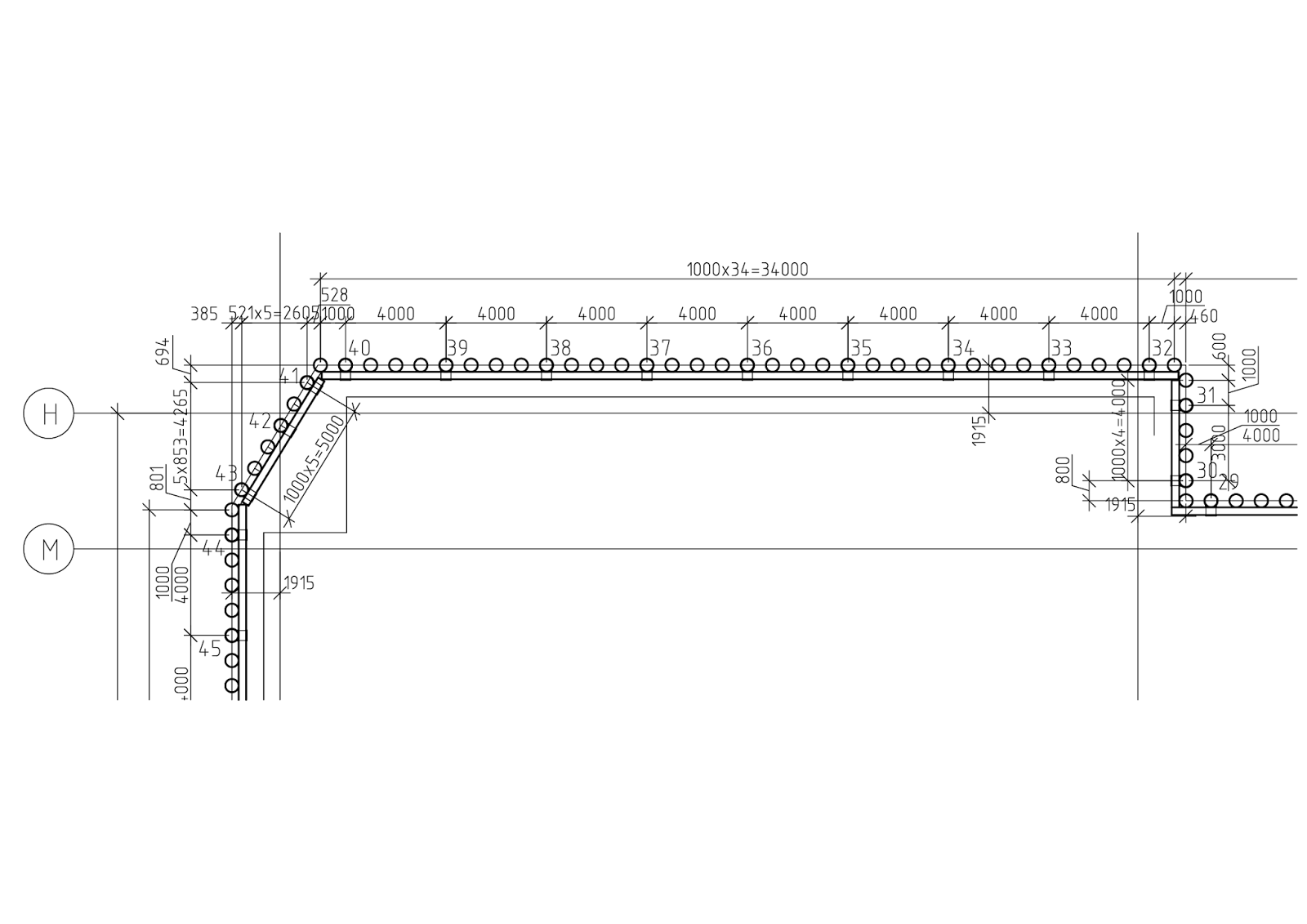 Специализацией нашей компании является геотехническое обоснование строительства,
Специализацией нашей компании является геотехническое обоснование строительства,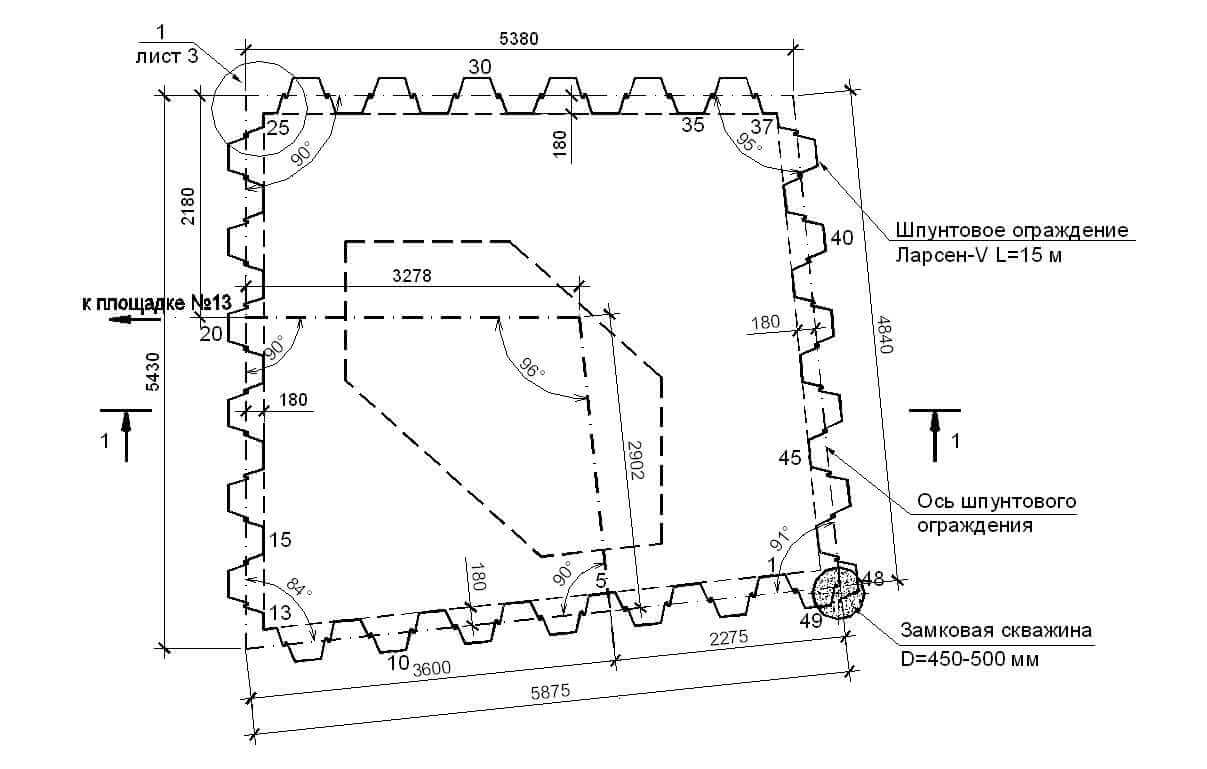 Проверка адекватности параметров, полученных геологами.
Проверка адекватности параметров, полученных геологами. Позволяет сопоставить результаты геотехнических расчетов с реальностью выполнения проекта шпунтового ограждения котлована в жизнь.
Позволяет сопоставить результаты геотехнических расчетов с реальностью выполнения проекта шпунтового ограждения котлована в жизнь.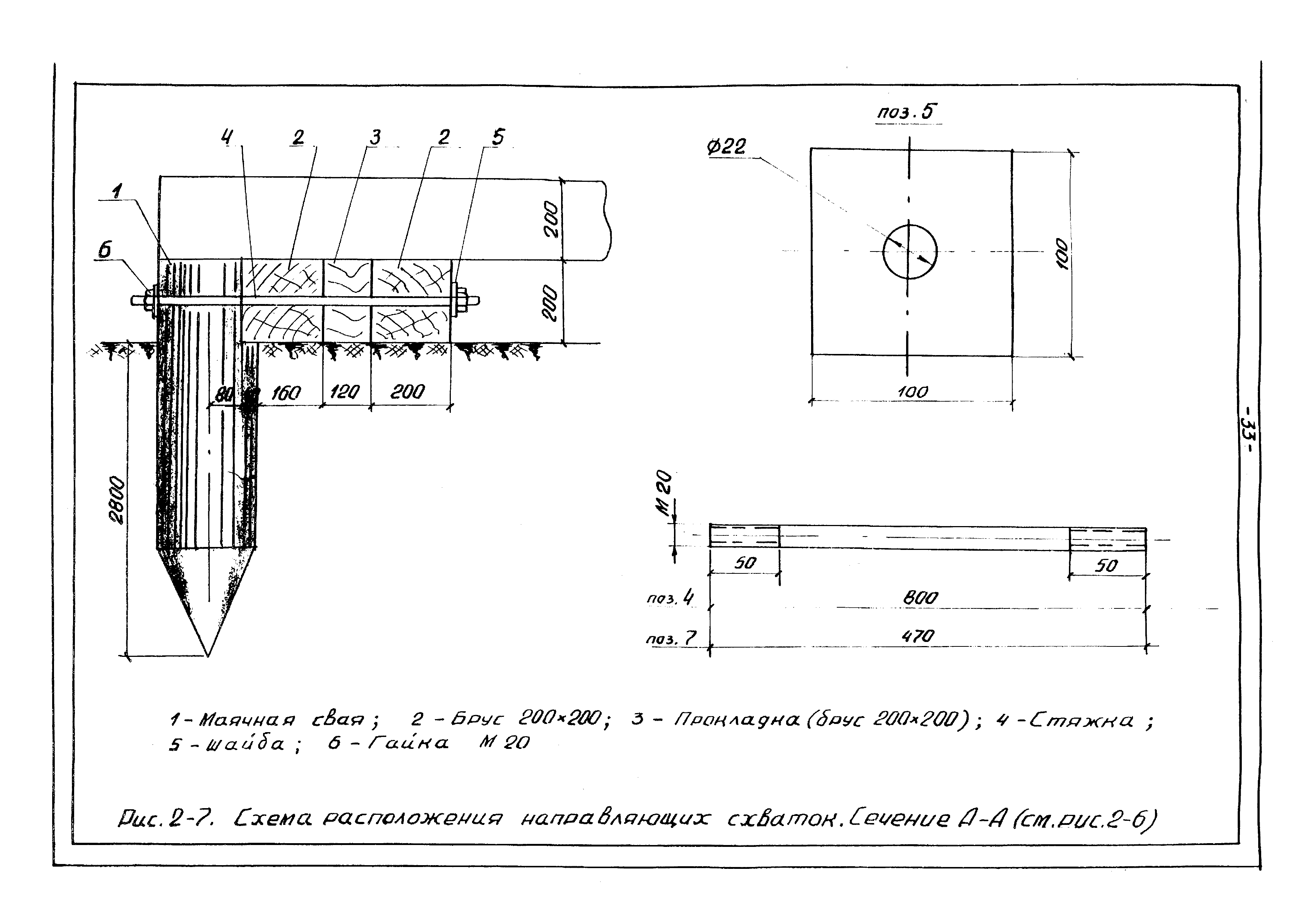 81
81 999
999 337
337 849
849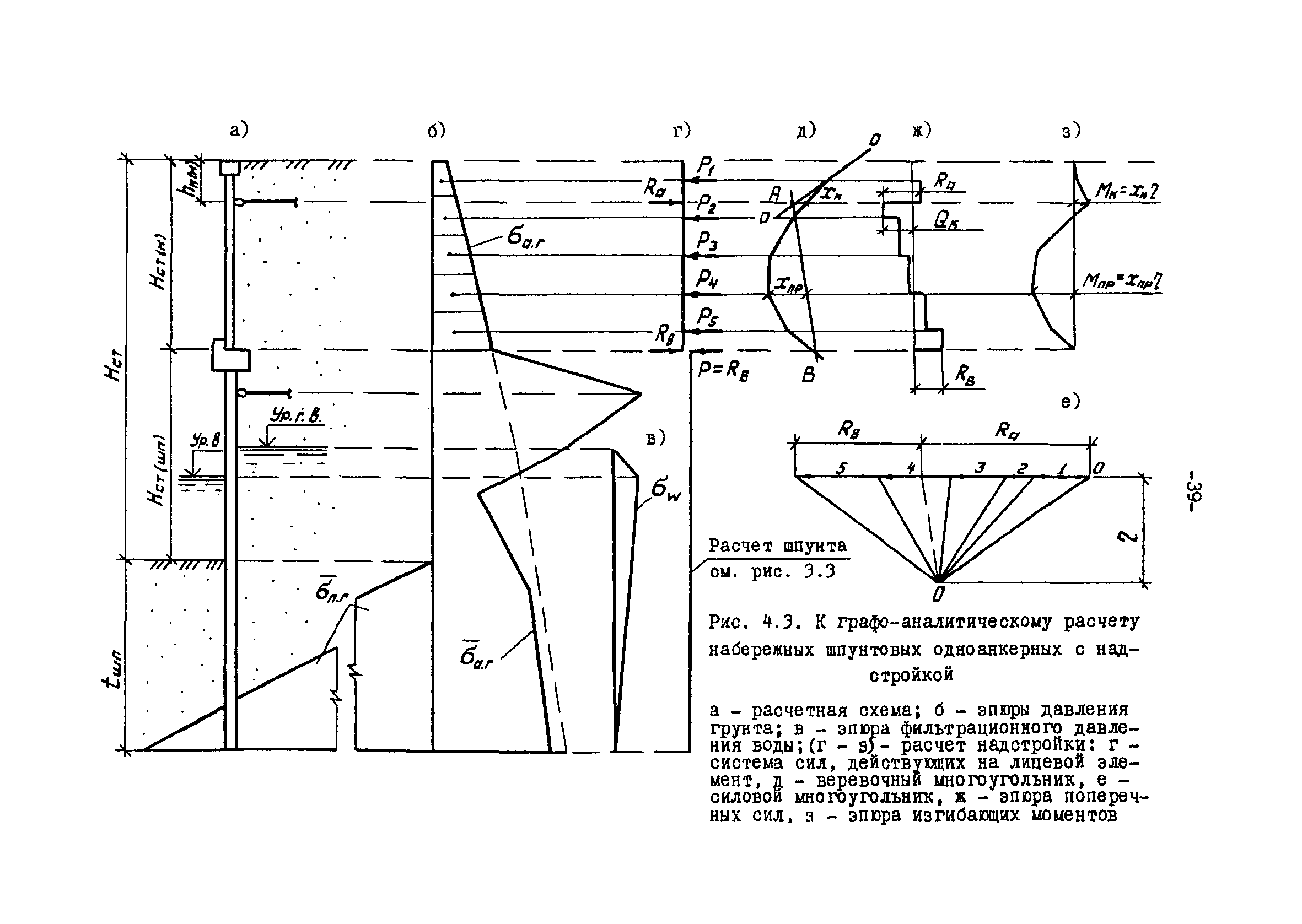 999
999 09
09 023
023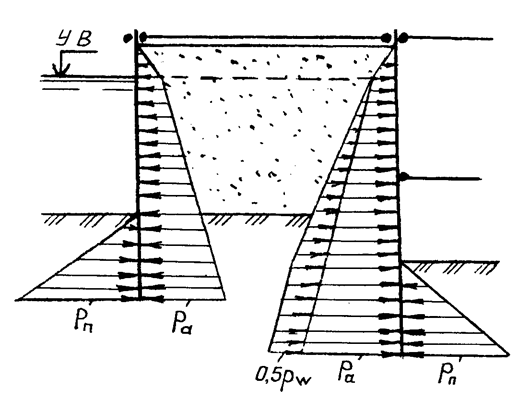 8.2.1
8.2.1 099
099 453 Т*м
453 Т*м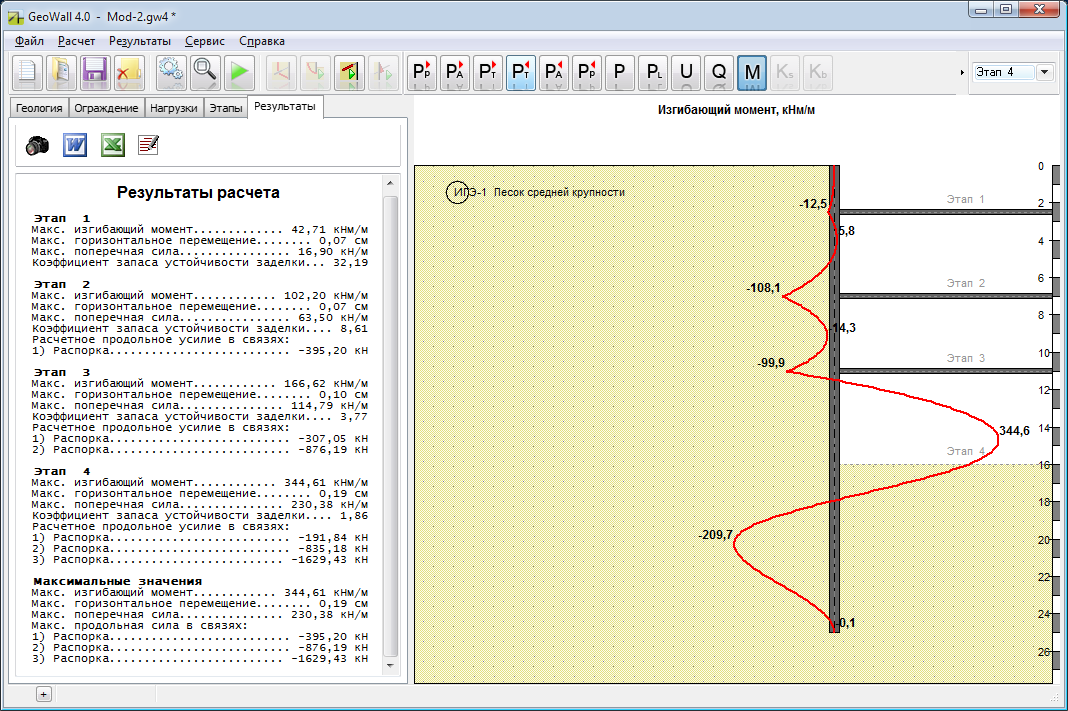 589
589 264
264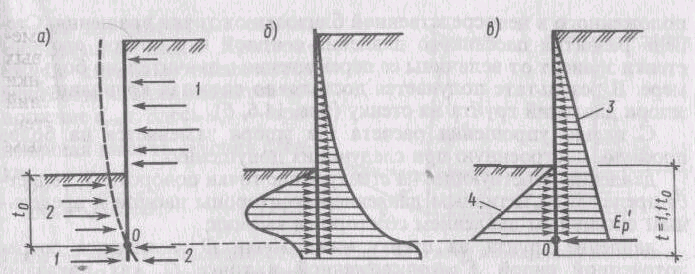 187
187 7
7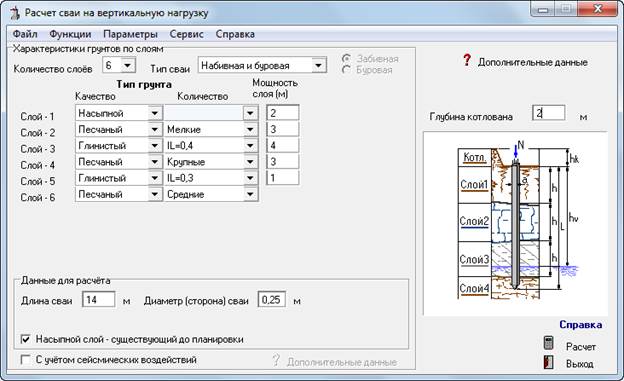 2
2 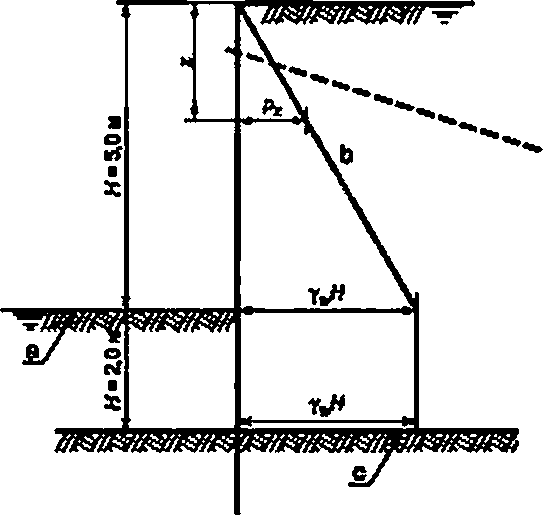 Единица силы – кН; единица длины м; единица крутящего момента – кН·м.
Единица силы – кН; единица длины м; единица крутящего момента – кН·м.
Добавить комментарий