Тренировочные варианты, геометрия, 11 класс
Варианты для подготовки к ЕГЭ (задания по геометрии)
Вариант № 1
1. Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 800 м и 300 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.
2. Электрику ростом 1,8 метра нужно поменять лампочку, закреплённую на стене дома на высоте 4,2 м. Для этого у него есть лестница длиной 3 метра. На каком наибольшем расстоянии от стены должен быть установлен нижний конец лестницы, чтобы с последней ступеньки электрик дотянулся до лампочки? Ответ запишите в метрах.
3. Квартира состоит из двух комнат, кухни, коридора и санузла (см. чертёж). Первая комната имеет размеры 4 м × 4 м, вторая — 4 м × 3,5 м, кухня имеет размеры 4 м × 3,5 м, санузел — 2 м × 1,5 м.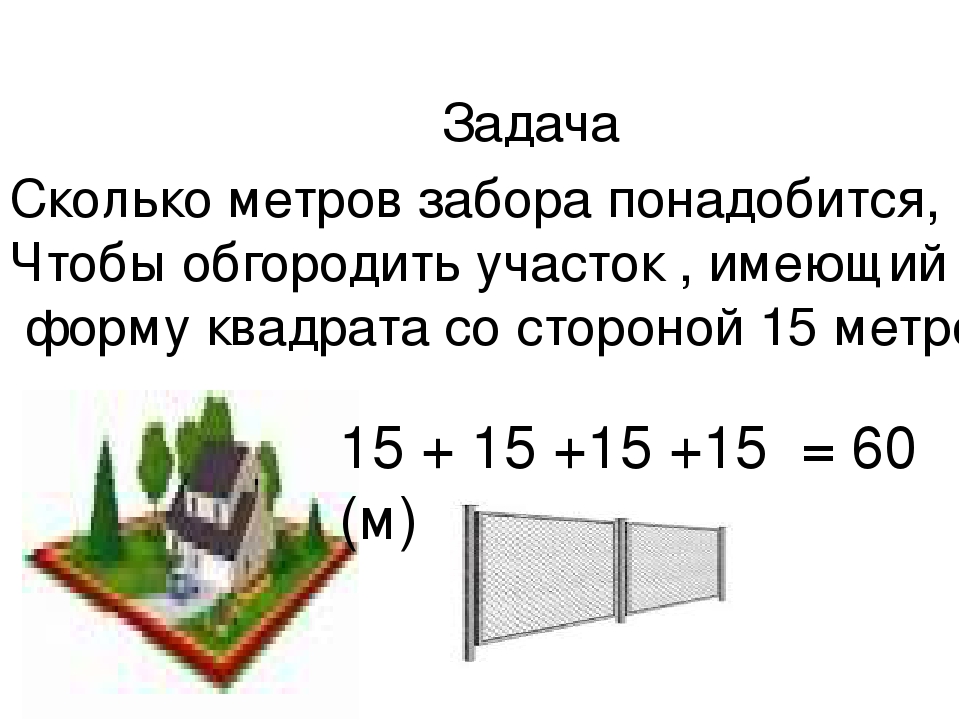
4. Детская горка укреплена вертикальным столбом, расположенным посередине спуска. Найдите высоту l этого столба, если высота h горки равна 2 метрам. Ответ дайте в метрах.
5. Участок земли имеет прямоугольную форму. Стороны прямоугольника 25 м и 70 м. Найдите длину забора (в метрах), которым нужно огородить участок, если в заборе нужно предусмотреть ворота шириной 4 м.
6.
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 15 метров. Хозяин отгородил на участке квадратный вольер со стороной 8 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
7. Дачный участок имеет форму прямоугольника со сторонами 20 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите общую длину забора в метрах.
Найдите общую длину забора в метрах.
8. Детская горка укреплена вертикальным столбом, расположенным посередине спуска. Найдите высоту
9. Пол в комнате, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 30 см. Сколько потребуется таких дощечек?
10. Участок земли имеет прямоугольную форму. Стороны прямоугольника 30 м и 60 м. Найдите длину забора (в метрах), которым нужно огородить участок, если в заборе нужно предусмотреть ворота шириной 3 м.
11.
12. Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.
13. Плоскость, проходящая через точки A, B и C, рассекает тетраэдр на два многогранника (см. рисунок). Сколько вершин у получившегося многогранника с большим числом граней?
Плоскость, проходящая через точки A, B и C, рассекает тетраэдр на два многогранника (см. рисунок). Сколько вершин у получившегося многогранника с большим числом граней?
14. В прямоугольном параллелепипеде известно, что , , . Найдите длину диагонали .
16.В бак цилиндрической формы, площадь основания которого равна 80 квадратным сантиметрам, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
17. Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
18.
19. Площадь боковой поверхности цилиндра равна , а высота — 1. Найдите диаметр основания.
20. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ключ Вариант № 1
№ п/п | Ответ |
1 | 1400 |
1,8 | |
3 | 66 |
4 | 1 |
5 | 186 |
6 | 311 |
7 | 120 |
8 | 1 |
9 | 800 |
10 | 177 |
11 | 24 |
12 | 72 |
13 | 6 |
14 | 27 |
15 | 60 |
16 | 1200 |
17 | 11 |
18 | 9 |
19 | 2 |
20 | 93 |
Вариант № 2
1. Участок земли для строительства дачи имеет форму прямоугольника, стороны которого равны 40 м и 30 м. Одна из больших сторон участка идёт вдоль реки, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.
Участок земли для строительства дачи имеет форму прямоугольника, стороны которого равны 40 м и 30 м. Одна из больших сторон участка идёт вдоль реки, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.
2. Квартира состоит из двух комнат, кухни, коридора и санузла (см. чертёж). Первая комната имеет размеры 3,5 м × 4,5 м, вторая — 3,5 м × 3 м, санузел имеет размеры 1,5 м × 2 м, длина коридора — 9 м. Найдите площадь всей квартиры (в квадратных метрах).
3. Диагональ прямоугольного телевизионного экрана равна 58 см, а ширина экрана — 42 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
4. Рыболовное хозяйство строит бассейн для разведения рыбы. Бассейн имеет форму прямоугольника со сторонами 4 м и 12 м. В центре бассейна находится техническая постройка, которая имеет форму прямоугольника со сторонами 2 м и 3 м.
5. Участок земли имеет прямоугольную форму. Стороны прямоугольника 25 м и 70 м. Найдите длину забора (в метрах), которым нужно огородить участок, если в заборе нужно предусмотреть ворота шириной 4 м.
6.
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 30 м и 75 м. Найдите длину забора (в метрах), которым нужно огородить участок, если в заборе предусмотрен проезд шириной 4 м.
7. План местности разбит на клетки. Каждая клетка обозначает квадрат 1м × 1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
8. Дачный участок имеет форму прямоугольника, стороны которого равны 40 м и 50 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 9 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
Ответ дайте в квадратных метрах.
9. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
10. Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 0,7 м, а наибольшая h2 равна 1,5 м. Ответ дайте в метрах.
11. Высота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса.
12. Конус вписан в цилиндр. Объем конуса равен 21. Найдите объем цилиндра.
13.
В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём сосуда 960 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
14. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 3 и 4, и боковым ребром, равным 3.
15. Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
16. В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 2 см. Ответ дайте в кубических сантиметрах.
17. В цилиндрический сосуд налили 5000 см3 воды. Уровень воды при этом достигает высоты 14 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 7 см. Чему равен объем детали? Ответ выразите в .
18. В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна 4; объем пирамиды равен 6. Найдите длину отрезка .
Найдите длину отрезка .
19. Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
20.
К правильной шестиугольной призме с ребром основания 1 приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что основания совпали. Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Ключ
№ п/п | Вариант № 1 | Вариант № 2 |
1 | 1400 | 100 |
2 | 1,8 | 55 |
3 | 66 | 40 |
4 | 1 | 42 |
5 | 186 | 186 |
6 | 311 | 206 |
7 | 120 | 12 |
8 | 1 | 1919 |
9 | 800 | 120 |
10 | 177 | 1,1 |
11 | 24 | 17 |
12 | 72 | 63 |
13 | 6 | 120 |
14 | 27 | 42 |
15 | 60 | 11 |
16 | 1200 | 3200 |
17 | 11 | 2500 |
18 | 9 | 4,5 |
19 | 2 | 48 |
20 | 93 | 13 |
Задача № Требуется огородить забором прямоугольный участок земли площадью в 294 и разделить затем этот участок забором на две равные части.
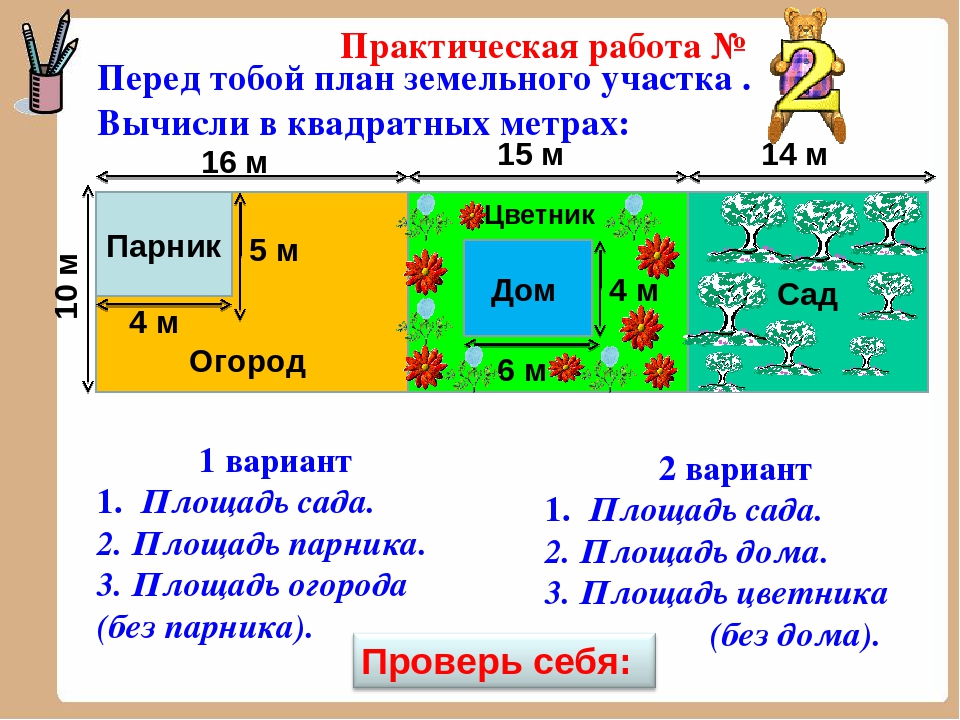 При каких линейных размерах участка длина всего забора окажется наименьшей? Задача №2 Задача № 1. Требуется огородить забором прямоугольный участок земли площадью в 294 и разделить затем этот участок забором на две равные части. При каких линейных размерах участка длина всего забора окажется наименьшей?
При каких линейных размерах участка длина всего забора окажется наименьшей? Задача №2 Задача № 1. Требуется огородить забором прямоугольный участок земли площадью в 294 и разделить затем этот участок забором на две равные части. При каких линейных размерах участка длина всего забора окажется наименьшей? Задача № 2. Прямоугольный лист жести имеет линейные размеры 5х8 дм. В четырех его углах вырезают одинаковые квадраты и делают открытую коробку, загибая края под прямым углом. Какова наибольшая вместимость полученной коробки?
Задача № 3. В прямоугольный треугольник с гипотенузой 24 см. и углом вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть длины сторон прямоугольника, чтобы его площадь была наибольшей?
Задача № 4. Две стороны параллелограмма лежат на сторонах треугольника, а одна из его вершин принадлежит третьей стороне. При каких условиях площадь параллелограмма является наибольшей?
Задача № 5.
 Среди равнобедренных треугольников с данной боковой стороной а найти треугольник наибольшей площади.
Среди равнобедренных треугольников с данной боковой стороной а найти треугольник наибольшей площади. Задача № 6. Боковые стороны и меньшее основание трапеции имеют одинаковые длины – по 50 см. Найти размер ее большего основания, при котором площадь трапеции была бы наибольшей.
Задача № 7. Найти длины сторон прямоугольника наибольшей площади, вписанного в прямоугольный треугольник со сторонами 18, 24 и 30см. и имеющего с ним общий прямой угол.
Задача № 8. Определить длины сторон прямоугольника наибольшей площади, вписанного в прямоугольную трапецию с длинами оснований 24 и 8см. и длиной высоты 12см. (две вершины прямоугольника лежат на боковых сторонах трапеции, а две другие – на ее большем основании).
Задача № 9. Из пункта А на прогулку вышел пешеход со скоростью v км/час. После того как он отошел от А на 6км., из А следом за ним выехал велосипедист, скорость которого была на 9км/час больше скорости пешехода.
 Когда велосипедист догнал пешехода, они повернули назад возвратились вместе в А со скоростью 4 км/час. При каком значении v время прогулки пешехода окажется наименьшим?
Когда велосипедист догнал пешехода, они повернули назад возвратились вместе в А со скоростью 4 км/час. При каком значении v время прогулки пешехода окажется наименьшим? Задача № 10. В равнобедренный треугольник с длинами сторон 15, 15 и 18см. вписан параллелограмм наибольшей площади так, что угол при основании у них общий. Найти длины сторон параллелограмма.
Задача № 11. В какой круг можно вписать прямоугольник наибольшей площадью с периметром, равным 56см.
Задача № 12. Боковая сторона равнобедренной трапеции равна ее меньшему основанию. Каков должен быть угол при большем основании, чтобы площадь трапеции была наибольшей?
Задача № 13. Величина угла при вершине А трапеции ABCD равна . Длина боковой стороны АВ вдвое больше длины меньшего основания ВС. При каком значении величина угла ВАС будет наибольшей?
Задача № 14. Найти косинус угла при вершине равнобедренного треугольника, имеющего наибольшую площадь при данной постоянной длине медианы, проведенной к его боковой стороне.

Задача № 15. Величина угла при основании равнобедренного треугольника равна . При каком значении отношение длин радиусов вписанной и описанной окружностей является наибольшим? Чему равно наибольшее значение этого отношения?
Задача № 16. Какие размеры нужно придать радиусу основания и высоте открытого цилиндрического бака, чтобы при данном объеме V на его изготовление пошло наименьшее количество листового металла?
Задача № 17. Боковая грань правильной четырехугольной пирамиды имеет постоянную заданную площадь и наклонена к плоскости основания под углом . При каком значении объем пирамиды является наибольшим?
Задача № 18. В правильную четырехугольную пирамиду с ребром основания а и высотой Н вписана правильная четырехугольная призма так, что ее нижнее основание лежит в основании пирамиды, а вершины верхнего основания – на боковых ребрах. Найти длину ребра основания и длину высоты призмы, имеющей наибольшую боковую поверхность.
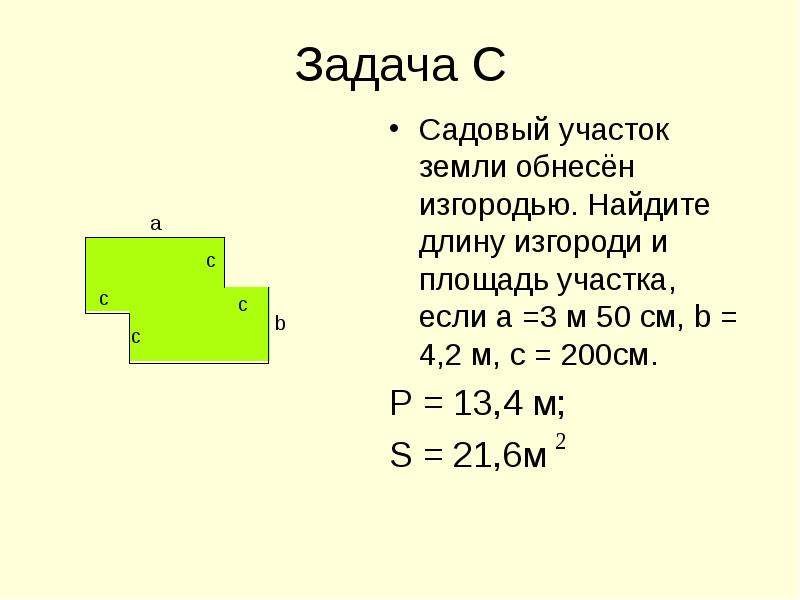
Задача № 19. Боковое ребро правильной треугольной пирамиды имеет постоянную заданную длину и составляет с плоскостью основания угол . При каком значении объем пирамиды является наибольшим?
Задача № 20. В правильной треугольной пирамиде боковая грань имеет заданную постоянную площадь и составляет с плоскостью основания угол . При каком значении расстояние от центра основания пирамиды до ее боковой грани является наибольшим?
Задача № 21. В конус с заданным постоянным объемом вписана пирамида; в ее основании лежит равнобедренный треугольник, у которого величина угла при вершине равна . При каком значении объем пирамиды является наибольшим?
Задача № 22. Образующая конуса имеет постоянную длину и составляет с высотой конуса угол . В конус вписана правильная шестиугольная призма с равными длинами ребер (основание призмы лежит в плоскости основания конуса). При каком значении боковая поверхность призмы является наибольшей?
Решение к задаче № 1.
Решение к задаче № 5.
| Пусть в равнобедренном ; площадь этого треугольника , будет наибольшей при . Ответ: равнобедренный прямоугольный треугольник с катетами а, а. | В х А С |
Решение к задаче № 14.
| Пусть в . По теореме косинусов Площадь . при . Таким образом, площадь треугольника АВС будет наибольшей, если . Ответ: | В
l А С |
Формула нахождения длины периметра прямоугольника. Периметр и площадь прямоугольника
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.
Основные понятия
Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника, например, поверхность стола, тетрадь и прочее.
Рассмотрим пример: по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.
Для того чтобы узнать длину каждой из сторон необходимо их измерить.
Рис. 1. Земельный участок формой прямоугольника.
Земельный участок имеет стороны длиной 2 м., 4 м., 2 м., 4 м. потому чтобы общую узнать длину забора необходимо сложить длины всех сторон:
2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.
Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют букву P.
Для вычисления периметра прямоугольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.
Периметр прямоугольника измеряется в мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одинаковую систему измерения.
Периметр прямоугольника измеряется в различных единицах: мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одну систему измерения.
Формула периметра фигуры
Если принять к вниманию тот факт, что противоположные стороны прямоугольника равны, то можно вывести формула периметра прямоугольника:
$P = (a+b) * 2$, где а, b – стороны фигуры.
Рис. 2. Прямоугольник, с обозначенными противоположными сторонами.
Существует и другой способ найти периметр. Если в задание дано лишь одну сторону и площадь фигуры, можно использовать выразить другую сторону через площадь. Тогда формула будет выглядеть следующим образом:
$P = {{2S + 2a2}\over{a}}$, где S – площадь прямоугольника.
Рис. 3. Прямоугольник с сторонами a, b .
Задание : Вычислить периметр прямоугольника, если его стороны равны 4 см. и 6 см.
Решение:
Используем формулу $P = (a+b)*2$
$P = (4+6)*2=20 см$
Таким образом, периметр фигуры $P = 20 см$.
Так как периметр – это сумма все сторон фигуры, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.
Чтобы получить периметр необходимо полупериметр умножить на 2.
Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.
Что мы узнали?
Мы узнали, как найти периметр прямоугольника. А также ознакомились с формулой его вычисления. С этой темой можно столкнуться не только при решении математических задач, но и в реальной жизни.
Тест по теме
Оценка статьи
Средняя оценка: 4.5 . Всего получено оценок: 363.
Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:
Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.
Периметр – это общая длина всех сторон фигуры.
Вычисление периметра прямоугольника — довольно простая задача.
Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.
Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.
P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.
Так же периметр прямоугольника можно найти при помощи суммы всех сторон.
P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.
Периметр квадрата — это длина стороны квадрата, умноженная на 4.
P = a 4, где a — длина стороны квадрата.
Дополнение: Нахождение найти площади и периметра прямоугольников
В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.
Основные понятия
Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:
- Прямой угол.
 Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника. - Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
- Квадрат. Является четырехугольником, все стороны которого равны.
При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.
Вычисление периметра
Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.
Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».
Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.
Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).
Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».
Ответ: P=5+4+3=12 (см).
Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».
Ответ: P=7+9+7+9=32 (см).
Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».
В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.
Ответ: 50 (м).
Вычисление площади
Более сложной величиной является площадь фигуры. Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.
Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².
Области применения единиц измерения могут быть такими:
- В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
- В дм² можно измерить географическую карту, оконное стекло, картину.
- Для измерения пола, квартиры, земельного участка используют м².
Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.
Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду. После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.
Значит, площадь прямоугольника — это произведение его длины и ширины.
Способы сравнения площадей:
- На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
- Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
- По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
- Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².
Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.
Ответ: 30 (м).
Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».
Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).
Ответ: 18 (м²).
Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон.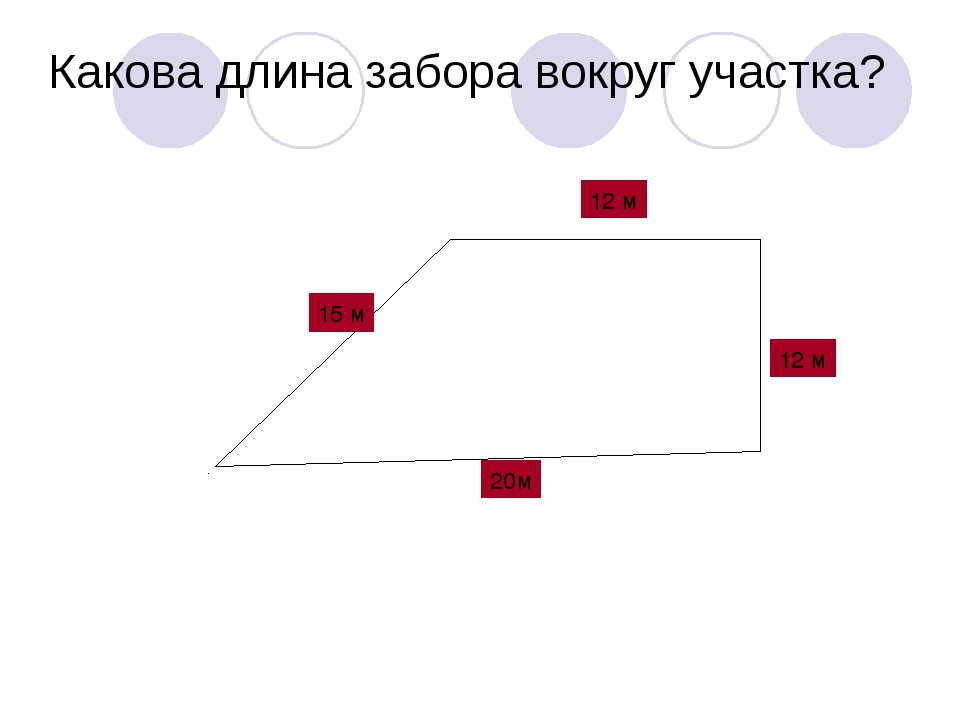 У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.

- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.
При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя .
В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. (1 + 9) * 2 = 20 точно также как и (2 + 8) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.
Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S 1 = 1 * 9 = 9 см 2
S 2 = 2 * 8 = 16 см 2
S 3 = 3 * 7 = 21 см 2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.
Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
В этом уроке:
- Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Задача 1. Найти стороны прямоугольника из площади
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров. Найдите стороны прямоугольника.Решение.
2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x 2 +2y 2 =260
x+y=16
x=16-y
2(16-y) 2 +2y 2 =260
2(256-32y+y 2)+2y 2 =260
512-64y+4y 2 -260=0
4y 2 -64y+252=0
D=4096-16×252=64
x 1 =9
x 2 =7
Теперь примем во внимание, что исходя из того, что x+y=16 (см.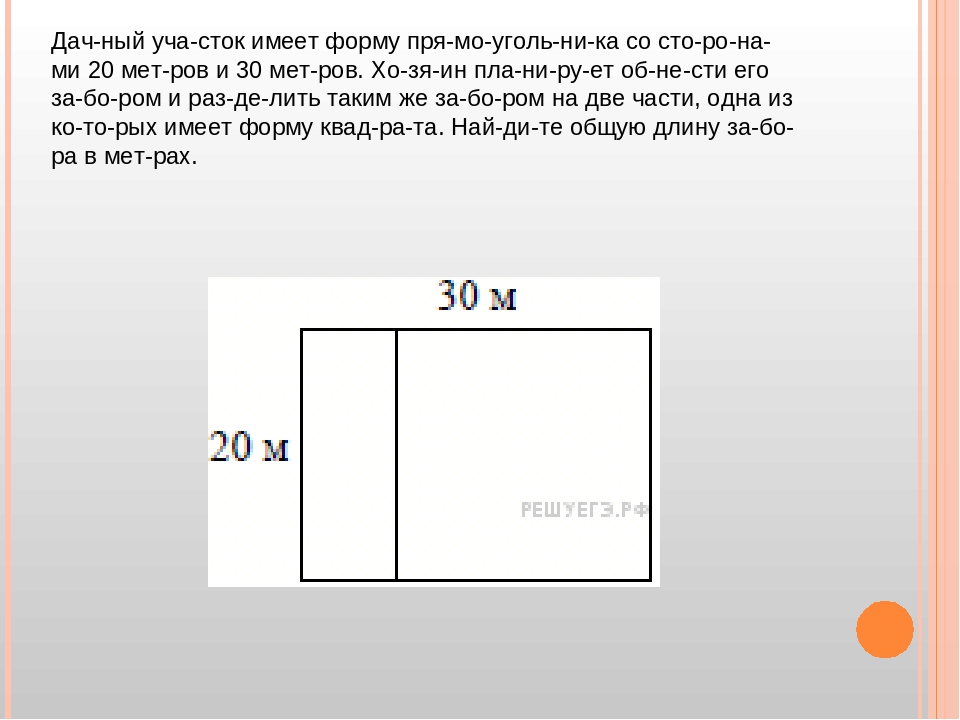 выше) при x=9, то y=7 и наоборот, если x=7, то y=9
выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ : Стороны прямоугольника равны 7 и 9 сантиметров
Задача 2. Найти стороны прямоугольника из периметра
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x 2 +y 2 =89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y) 2 +y 2 =89
169-26y+y 2 +y 2 -89=0
2y 2 -26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x 1 =5
x 2 =8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см
Задача 3. Найти площадь прямоугольника из пропорции его сторон
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.
Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см 2
Решение .
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a 2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S 2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S 2 = S / 1. 25
25
S 2 = 1,25ab / 1.25
Поскольку новый размер а изменять нельзя, то
S 2 = (1,25a) b / 1.25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на (1 — 0,8) * 100% = 20%
Ответ : ширину нужно уменьшить на 20%.
Компания «Яркие заборы». Евроштакетник от производителя!
За последние годы дачное и коттеджное строительство серьезно набрало обороты. Первое, с чем сталкивается будущий владелец загородного дома, это какой купить забор и кто выполнит монтаж забора.
Мы, компания «Яркие заборы», производим и реализуем в Красноярске и Красноярском крае евроштакетник, как еще называют этот продукт — металлический штакетник.
Проезжая по современным поселкам мы уже начали замечать заборы из металлических реек, которые имеют, как правило яркие цвета и интересные формы. Да, это заборы из евроштакетника и они по-настоящему дают возможность разгуляться фантазии при выборе — цвета забора, формы металлического штакетника и типа обработки верхнего торца евроштакетника. Некоторые наши клиенты жалуются на заборы из профлиста при этом рассказывая про серьезные минусы данных заборов.
Некоторые наши клиенты жалуются на заборы из профлиста при этом рассказывая про серьезные минусы данных заборов.
Минусы заборов из профлиста:
- Большая парусность
- Внутри закрытого наглухо забора некомфортно
- Отсутствует продуваемость участка, плохие урожаи
- Отсутствует возможность интересных комбинаций цвета забора
Данные недостатки полностью удается решить выбрав забор из евроштакетника.
Если вы собираетесь построить забор своими руками, то евроштакетник, пожалуй идеальный и удобный материал для забора, так как имеет ряд преимуществ.
Преимущества забора из евроштакетника:
- Продуваемость участка – отличные урожаи и можно использовать для каркаса забора трубы меньшего сечения.
- Возможность выбирать при монтаже зазор между металлическим штакетником и самим задавать «прозрачность» забора.
- Забор из евроштакетника дает возможность построить забор абсолютно индивидуальный, выбирая основные параметры: длина, цвет и тип верхней кромки профиля для забора.

- Монтируя евроштакетник разной длины на одном заборе, можно добиться оригинального внешнего вида ограды в виде морской волны или елочки, например.
- Габаритный размер евроштакетника позволяет его перевозить в легковом автомобиле, а монтаж металлического штакетника своими руками возможен, благодаря простому способу крепления на саморезы или заклепки.
Теперь купить евроштакетник от производителя можно в городе Красноярске с минимальной наценкой. Обращайтесь в компанию «Яркие заборы», мы будем рады изготовить качественный евроштакетник для Вас!
Главная / Транспортная компания Луч
Здравствуй, уважаемый Клиент!
Мы рады приветствовать Вас на официальном сайте Транспортной компании «Луч».
Транспортная компания «Луч» – уникальная и единственная компания, которая специализируется на ежедневных срочных доставках Ваших грузов во все уголки Челябинской, Свердловской, Тюменской, Курганской областей, Пермского края, Ханты-Мансийского автономного округа, Республики Башкортостан, а также Республики Казахстан!
Собственный, динамично увеличивающийся автопарк — одно из наших безусловных преимуществ на постоянно растущем рынке внутренних и международных грузоперевозок. Мы являемся конечными перевозчиками, а не диспетчерами, поэтому мы гарантируем минимальные цены при сохранении максимально коротких сроков доставки. Чтобы предложить уникальные условия доставки Ваших грузов мы располагаем широким разнообразием автотранспортных средств: начиная с автомобилей объемом кузова от 16 куб. м. при длине 4 метра, и, заканчивая полноценными седельными тягачами с полуприцепами объемом в 91 куб. м. при длине 13,5 метров. Это позволяет поставить по запросу автотранспортное средство, которое полностью подойдет под любые Ваши нужды, в любой город нашего присутствия
Мы являемся конечными перевозчиками, а не диспетчерами, поэтому мы гарантируем минимальные цены при сохранении максимально коротких сроков доставки. Чтобы предложить уникальные условия доставки Ваших грузов мы располагаем широким разнообразием автотранспортных средств: начиная с автомобилей объемом кузова от 16 куб. м. при длине 4 метра, и, заканчивая полноценными седельными тягачами с полуприцепами объемом в 91 куб. м. при длине 13,5 метров. Это позволяет поставить по запросу автотранспортное средство, которое полностью подойдет под любые Ваши нужды, в любой город нашего присутствия
Уникальные маршруты для нашего региона — визитная карточка Транспортной Компании «Луч»:
- Закрытые города (с пропуском, склад непосредственно в городе):
- -Снежинск
- -Озерск
- -Трехгорный
- Крупные города Челябинской области – ДВА раза в день!:
- -Миасс
- -Златоуст
- -Южноуральск
- -Троицк
- -Озерск
- -Снежинск
- Границу с Республикой Казахстан наши машины проходят в «легковой» очереди, отдельно от большегрузного транспорта.
 Это существенно снижает время прохождения таможни, а значит увеличивает скорость доставки груза!
Это существенно снижает время прохождения таможни, а значит увеличивает скорость доставки груза!
Для Вас разработаны очень удобные и незаменимые сервисы, которые наши постоянные клиенты уже оценили и успешно применяют их при заказе грузоперевозки в нашей компании. Ознакомиться с ними Вы можете в главном меню в подразделе «Услуги».
Уважаемые клиенты, так как мы перевозим грузы со скоростью экспресс-почты по ценам, которые Вас приятно удивят, рекомендуем Вам ознакомиться с правилами работы нашей компании и тарифами на грузоперевозки.
Если у Вас есть предложения по улучшению качества работы нашей компании, ты мы с удовольствием ознакомимся с ними в разделе контроля качества и связи с руководством Транспортной компании «Луч».
Расширяйте географию Вашего бизнеса с Транспортной компанией «Луч»!
Штакетник металлический в Шымкенте по цене производителя
1000
Зелёно-бежевый
1001
Бежевый
1002
Песочный
1003
Сигнальный жёлтый
1004
Золотой
1005
Медовый
1006
Кукурузный
1007
Нарциссовый
1011
Коричнево-бежевый
1012
Лимонный
1013
Жемчужно-белый
1016
Жёлтая сера
1017
Шафрановый
1018
Цинковый
1019
Серо-бежевый
1020
Оливковый
1021
Рапсовый
1023
Транспортно-жёлтый
1024
Охра жёлтая
1028
Дынный
2000
Жёлто-оранжевый
2004
Оранжевый
2011
Насыщенный оранжевый
3011
Коричнево-красный
3028
Красный
5002
Ультрамариново-синий
5003
Сапфирово-синий
6021
Бледно-зелёный
6029
Мятно-зелёный
7001
Серебристо-серый
7040
Серое окно
7044
Серый шёлк
8003
Глиняный коричневый
9006
Бело-алюминиевый
9007
Тёмно-алюминиевый
9010
Белый
9011
Графитно-чёрный
9016
Транспортный белый
9017
Транспортный чёрный
9018
Папирусно-белый
9022
Перламутровый светло-серый
9023
Перламутровый тёмно-серый
«Вести недели» показали виллу, где жил Навальный в Германии.
 Геленджикскому дворцу противопоставили блестящий ершик и общий бассейн — Общество — Новости Санкт-ПетербургаФото: скриншот с сайта YouTube
Геленджикскому дворцу противопоставили блестящий ершик и общий бассейн — Общество — Новости Санкт-ПетербургаФото: скриншот с сайта YouTubeЖурналисты телеканала «Россия 1» съездили в немецкий Фрайбург и нашли дом, в котором жил Алексей Навальный, пока готовился фильм про дворец в Геленджике. Ему насчитали до миллиона евро расходов.
Дом в городе Фрайбург государственный телеканал показал вечером 7 февраля. Корреспондент Анастасия Попова сначала посетила студию Black forest studios, на которой снимали и монтировали последний фильм-расследование Фонда борьбы с коррупцией (фонд признан в России иноагентом. — Прим. ред.). В сюжете говорится, что заказ студии пришел из США, а съемки стоили Навальному почти миллион евро — за вычетом расходов на проживание и еду.
«Внизу около ста квадратных метров, просторная гостиная, два дивана, телевизор, на столе свежие фрукты», — рассказывает за кадром Попова, показывая тот самый дом.
Сюжет перебивается кадрами из фильма Навального. Анастасия Попова обозревает кухню с кофемашиной и «набором голландского чая», заглядывает и в «комнату грязи» — подсобное помещение.
Анастасия Попова обозревает кухню с кофемашиной и «набором голландского чая», заглядывает и в «комнату грязи» — подсобное помещение.
Следующий кадр из уборной, там девушка оценила унитаз, по ее мнению, похожий на те, что стоят в вагонах поездов, и ершик. «Блестит, но не так», — комментирует она.
Затем сотрудница госканала показала джакузи, «который похож на обычную ванну», и поплавала в бассейне. «Пациент и себя не обделил, десять метров в длину, пять в ширину», — говорит Попова после очередной врезки кино ФБК. — «Вода теплая».
На втором этаже «печка, на которую не прилечь» и «камин за кожаным диваном», а также шикарный вид из окна. Как отметила Попова, на фоне этого вида оппозиционер записывал ролик с анонсом своего возвращения.
В гардеробной Попова обратила внимание на то, что все шкафы обиты тканью, а в замках «сказочные золотые ключики». «Французский стиль 60-х», — вставила комментарий Анастасия. Вместе с хозяином дома они обозрели шкаф для обуви, немец объясняет, что во Фрайбурге очень много обувных магазинов.
Попова сообщила, что сутки на вилле обходятся в 530 евро, а прожил Навальный там почти два месяца. Цена, заявленная в сюжете, совпадает с той, что предлагает сервис бронирования Booking, но такую плату берут за двое суток.
Соратники Алексея Навального 19 января выпустили фильм о дворце в Геленджике, утверждая, что недвижимость площадью больше 17 тыс. кв. м строится для Владимира Путина. В видео использовали якобы полученный от подрядчика «детальный архитектурный план», по которому воссоздали внешнее и внутреннее убранство. «Мы заказали 3D-визуализацию и воссоздали все интерьеры», — так сам Алексей Навальный прокомментировал методы их работы. Президент России Владимир Путин заявил, что ни он, ни его родственники никогда не владели геленджикским дворцом. А еще через неделю хозяином дома себя назвал российский миллиардер Аркадий Ротенберг, уточнив, что идет строительство апарт-отеля.
Fence It
Есть много способов решить эту проблему, и мы получили много отличных ответов. Поскольку вопросы становятся все сложнее и сложнее, давайте начнем с первой проблемы.
Поскольку вопросы становятся все сложнее и сложнее, давайте начнем с первой проблемы.Какой самый большой прямоугольный участок земли можно отгородить 40-метровым забором?
Эми испробовала множество возможных длин сторон прямоугольника. Она использовала формулу основания, умноженного на высоту, чтобы получить площадь.
| цоколь (м) | высота (м) | площадь (м 2 ) |
| 10 | 10 | 100 |
| 9 | 11 | 99 |
| 5 | 15 | 75 |
| 1 | 19 | 19 |
Исходя из этого, я думаю, что ответ будет 100 м 2 , потому что таблица показывает меньше
промежуток между двумя числами больше площадь и нет промежутка
между 10 и 10, так что это должны быть они.
Это рассуждение звучит правильно, молодец. Не волнуйтесь, что при высоте основания 10 м отгороженная территория образует квадрат; квадрат — это просто особый вид прямоугольника! Если мы немного подумаем, сможем ли мы быть абсолютно уверены, что нет никакого способа улучшить 100m 2 ? Натан использовал буквы x и y, чтобы обозначить основание и высоту
прямоугольник.
Если стороны имеют длину x и y метров, то периметр прямоугольника равен 2x + 2y метров. Поскольку это все ограждение, которое мы можем использовать, мы должны иметь 2x + 2y = 40.Площадь прямоугольника x умножена на y, что я могу записать как xy.
Из первого уравнения мы знаем, что 2y = 40-2x, так что y = 20-x.
Тогда формулу для площади можно записать
xy = x (20-x) = 20x-x 2 .
Наибольшее значение, которое может принять выражение 20x-x 2 , равно 100, что соответствует x = 10.
Совершенно верно. Если вы нарисуете график функции 20x-x 2 , вы увидите, что она максимальна при x = 10 со значением 200. Существуют также продвинутые методы, которые могут помочь найти наивысшую точку, если вы не можете нарисовать график.
Действительно особый аргумент о симметрии звучит так: в уравнениях 2x + 2y = 40 и Area = xy нет ничего различного между x и y; вы можете поменять местами их имена, и уравнения будут такими же. Это часто означает, что значения x и y должны быть одинаковыми.
Это часто означает, что значения x и y должны быть одинаковыми.
Какую самую большую прямоугольную область можно отгородить стеной с одной стороны?
Braiden заметил следующее и составил список возможных решений.
Второй вопрос дает вам такое же количество секций забора, но необходимо заполнить только три стороны прямоугольника.
Формула количества забора по периметру: x + 2y = 40.
Область xy, как и раньше.
Обратите внимание на x = 40-2y, поэтому мы получаем:
Area = xy = (40-2y) y = 40y-2y 2 .
Теперь нарисуйте график или используйте передовые методы, чтобы найти наивысшую точку этой функции: 40 лет 2 .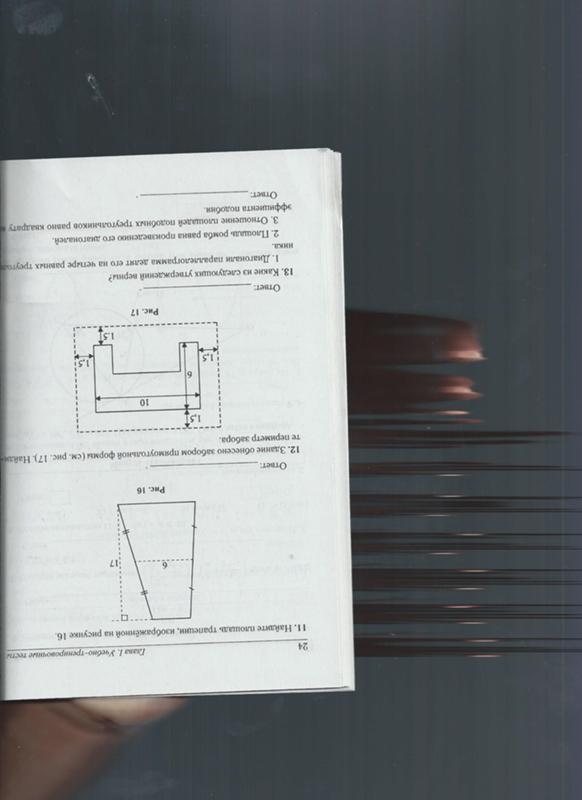 При y = 10 получаем площадь 200м 2 . Обратите внимание, что в данном случае x = 20, поэтому огражденная территория не является квадратом.
При y = 10 получаем площадь 200м 2 . Обратите внимание, что в данном случае x = 20, поэтому огражденная территория не является квадратом.
Какую самую большую площадь можно отгородить с отмеченной точкой крепления?
Эта третья проблема самая сложная, но и испытания, и улучшения, и алгебра могут помочь нам найти ответ. Каэдан заметил, что вы можете разделить область на более мелкие прямоугольники. Изображение ниже тоже может помочь.
Какая площадь покрыта с обозначенными сторонами? И какой длины используется забор? Нескольким людям удалось разобраться с этим, молодцы!
Первая площадь.У нас в нижнем левом углу 8х10 = 80м 2 .
У оставшегося прямоугольника длина основания x метров и высота y-10.
Тогда общая площадь равна 80 + x (y-10).
Это можно записать в виде Area = 80 + xy-10x.
Теперь по периметру. Мы используем y + x + y-10 метров забора. То есть x + 2y-10 = 40.
Некоторые люди составили таблицу значений, чтобы вычислить последний бит, и алгебра тоже работает.
Уравнение периметра означает, что x = 50-2y, поэтому уравнение площади равно
Area = 80 + 50y-2y 2 -500 + 20y = 70y-2y 2 -420.
Построив график или используя другой метод, мы можем увидеть, что наибольшее значение находится при y = 17,5. Это составляет 192,5 м 2 .
Пристройка: а как насчет изогнутых заборов?
Существует так много разных форм с изогнутыми сторонами, и вы можете не знать формулы площади для каждой из них. Попробуйте использовать несколько форм, площадь которых вам известна, и посмотрите, что у вас получится. Сможете ли вы превзойти лучшие значения, которые мы нашли, с прямоугольниками и прямыми сторонами? Вам нужны разные формы или всегда будет выигрывать одна?
садовый забор (задача оптимизации) — Матено.com
Задача оптимизации вычислений:
Какие размеры минимизируют стоимость садового забора?
Сэм хочет построить садовый забор, чтобы защитить прямоугольную территорию площадью 400 квадратных футов. Его ближайший сосед соглашается заплатить за половину забора, граничащего с ее собственностью; Сэм оплатит остальную часть стоимости. Какие размеры посадочной площадки минимизируют затраты Сэма на строительство забора? (Вы можете оставить свой ответ в виде квадратного корня; вам не нужно искать десятичный результат.)
Его ближайший сосед соглашается заплатить за половину забора, граничащего с ее собственностью; Сэм оплатит остальную часть стоимости. Какие размеры посадочной площадки минимизируют затраты Сэма на строительство забора? (Вы можете оставить свой ответ в виде квадратного корня; вам не нужно искать десятичный результат.)
Calculus Solution
Мы будем использовать нашу стандартную стратегию решения проблем оптимизации для разработки нашего решения. (Ссылка откроется в новой вкладке.)
Этап I: Разработка функции .Ваша первая задача — разработать функцию, которая представляет количество, которое вы хотите оптимизировать. Он может зависеть только от одной переменной . Шаги:
1. Нарисуйте картину физического состояния.
Смотрите рисунок. Мы назвали ширину сада x (верхняя и нижняя части забора) и длину сада x (левая и правая стороны).2 $.
2. Напишите уравнение, которое связывает количество, которое вы хотите оптимизировать, с точки зрения соответствующих переменных.
Мы хотим свести к минимуму затраты Сэма на строительство забора, что равносильно минимизации стоимости забора, за которую он платит. Назовем это стоимостью C . Помните, что Сэм оплачивает только половину стоимости правой стороны забора, так как его сосед платит за вторую половину. Затем
\ [\ begin {align *}
C & = \ text {(длина левой стороны)} + \ text {(длина верхней части)} + \ dfrac {1} {2} \ text {(длина правой стороны сторона)} + \ text {(длина низа)} \\ [8px]
& = y + x + \ dfrac {1} {2} y + x \\
& = \ dfrac {3} {2} y + 2x
\ end {align *} \]
3.При необходимости используйте другую предоставленную информацию, чтобы переписать уравнение в терминах одной переменной.
Стоимость C в настоящее время зависит от двух переменных: y и x . Чтобы продолжить, мы должны использовать другую информацию, которая нам дана, чтобы переписать область только с на из этих переменных. 2 $.Поскольку прямоугольная площадь сада равна
2 $.Поскольку прямоугольная площадь сада равна
$$ A = xy = 400 $$
, мы можем решить для y в терминах x :
$$ y = \ dfrac {400} {x} $$
Подставив это выражение для y в наше выражение выше для стоимости C :
\ [\ begin {align *}
C & = \ dfrac {3} {2} y + 2x \\ [8px]
& = \ dfrac {3} {2} \ left (\ dfrac {400} {x} \ right) + 2x \\ [8px]
& = \ frac {600} {x} + 2x
\ end {align *} \]
Выражение для C теперь является функцией единственной переменной x , если требуется.
Мы изобразили функцию, шаг, который вы, вероятно, не сделали бы сами, но мы хотим подчеркнуть, что все, что вы сделали до сих пор, — это создание функции, которую вы сейчас собираетесь минимизировать. Один из вариантов — внимательно изучить график, чтобы определить значение x , которое минимизирует C . . . но вместо этого мы собираемся использовать методы максимума / минимума, которые вы недавно изучили! Этап II: Увеличение или уменьшение функции.
 2}> 0 \ right) $.Следовательно, эта единственная критическая точка дает нам минимум затрат. C :
2}> 0 \ right) $.Следовательно, эта единственная критическая точка дает нам минимум затрат. C :Минимальные затраты возникают, когда $ x = \ sqrt {300} $ ft.
6. Определите максимумы и минимумы, если необходимо. Не забудьте проверить конечные точки, если они есть.
Напомним, что мы обнаружили выше, что $ y = \ dfrac {400} {x} $. Следовательно, когда ширина $ x = \ sqrt {300} $, длина сада y должна быть:
\ [\ begin {align *}
y & = \ frac {400} {x} \\ [8px]
& = \ frac {400} {\ sqrt {300}} \\ [8 пикселей]
& = \ frac {400} {\ sqrt {100} \ sqrt {3}} \\ [8 пикселей]
& = \ frac {400} {10 \ sqrt {3}} = \ frac {40} {\ sqrt {3}}
\ end {align *} \]
Следовательно, стоимость Сэма минимизируется, когда сад имеет ширину
$ x = \ sqrt {300} \ text {ft,} \ quad \ cmark $
и длину
$ y = \ dfrac {40} {\ sqrt {3 }} \ text {ft.} \ quad \ cmark $
7. Наконец, убедитесь, что вы ответили на вопрос в соответствии с заданным: значения $ x $ или $ y $, или координаты, или максимальная площадь, или кратчайшее время, или. . . .
Наконец, убедитесь, что вы ответили на вопрос в соответствии с заданным: значения $ x $ или $ y $, или координаты, или максимальная площадь, или кратчайшее время, или. . . .
В вопросе нам задали размеры сада, которые мы предоставили. $ \ checkmark $
Вернуться к проблемам оптимизации
Хотите получить доступ к всем нашим задачам и решениям? Купите полный доступ прямо сейчас — это быстро и просто!
Безопасность | Стеклянная дверь
Мы получаем подозрительную активность от вас или от кого-то, кто использует вашу интернет-сеть.Подождите, пока мы убедимся, что вы настоящий человек. Ваш контент появится в ближайшее время. Если вы продолжаете видеть это сообщение, напишите нам чтобы сообщить нам, что у вас проблемы.
Nous aider à garder Glassdoor sécurisée
Nous avons reçu des activités suspectes venant de quelqu’un utilisant votre réseau internet.
Подвеска Veuillez Patient que nous vérifions que vous êtes une vraie personne. Вотре содержание
apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un
электронная почта à
pour nous informer du désagrément.
Вотре содержание
apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un
электронная почта à
pour nous informer du désagrément.
Unterstützen Sie uns beim Schutz von Glassdoor
Wir haben einige verdächtige Aktivitäten von Ihnen oder von jemandem, der in ihrem Интернет-Netzwerk angemeldet ist, festgestellt. Bitte warten Sie, während wir überprüfen, ob Sie ein Mensch und kein Bot sind. Ihr Inhalt wird в Kürze angezeigt. Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте: .
We hebben verdachte activiteiten waargenomen op Glassdoor van iemand of iemand die uw internet netwerk deelt.Een momentje geduld totdat, мы исследовали, что u daadwerkelijk een persoon bent. Uw bijdrage zal spoedig te zien zijn. Als u deze melding blijft zien, электронная почта: om ons te laten weten dat uw проблема zich nog steeds voordoet.
Hemos estado detectando actividad sospechosa tuya o de alguien con quien compare tu red de Internet. Эспера
mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo
este mensaje, envía un correo electrónico
a para informarnos de
que tienes problemas.
Эспера
mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo
este mensaje, envía un correo electrónico
a para informarnos de
que tienes problemas.
Hemos estado percibiendo actividad sospechosa de ti o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para hacernos saber que estás teniendo problemas.
Temos Recebido algumas atividades suspeitas de voiceê ou de alguém que esteja usando a mesma rede. Aguarde enquanto confirmamos que Você é Uma Pessoa de Verdade.Сеу контексто апаресера эм бреве. Caso продолжить Recebendo esta mensagem, envie um email para пункт нет informar sobre o проблема.
Abbiamo notato alcune attività sospette da parte tua o di una persona che condivide la tua rete Internet.
Attendi mentre verifichiamo Che sei una persona reale. Il tuo contenuto verrà visualizzato a breve. Secontini
Visualizzare questo messaggio, invia un’e-mail all’indirizzo
per informarci del
проблема.
Secontini
Visualizzare questo messaggio, invia un’e-mail all’indirizzo
per informarci del
проблема.
Включите файлы cookie и перезагрузите страницу.
Это автоматический процесс. Ваш браузер в ближайшее время перенаправит вас на запрошенный контент.
Подождите до 5 секунд…
Заводское обозначение: CF-102 / 61e5e5a4dfa6f16a.
Сколько материала нужно для ограждения акра земли?
Подробнее: ресурсы для забора
Магазин: Забор из звеньев цепи | Декоративный забор | Виниловый забор | Деревянный забор
Часто клиенты хотят знать, сколько стоит оградить акр земли.Акр — это мера площади, тогда как при расчете материалов забора вы обычно имеете дело с определением периметра или расстояния вокруг собственности. По-прежнему довольно легко определить периметр, если вы знаете площадь своей собственности.
Один акр земли составляет 43 560 квадратных футов. Если вы предположите, что ваша собственность состоит из 4 равных сторон, то вы можете извлечь квадратный корень (√) из 43 560 и выяснить, что каждая сторона будет иметь размер 209 футов. Поскольку это основано на квадрате, вам потребуется 209 погонных футов на 4 стороны, чтобы получить 835 погонных футов забора, окружающего этот акр.
Пример 1 — Расчет количества забора для ограждения 1 акра земли:
1) Один акр = 43 560 квадратных футов
2) Чтобы найти длину одной стороны, вам понадобится квадратный корень (√) из 43 560, что равно 209 погонных футов
3) 209 (погонных футов) x 4 (стороны) = 836 погонных футов оградить 1 сотку.
У большинства людей нет точного акра, поэтому, если вы хотите вычислить несколько акров, умножьте 43 560 акров на количество акров, затем возьмите квадратный корень из этого произведения и умножьте его на 4, что даст вам общий размер в метражах. забора требуется.
Пример 2 — Расчет количества забора для ограждения 10 акров земли:
1) Один акр = 43560 квадратных футов
2) Десять акров = 10 x 43560 квадратных футов — или — 435 600 квадратных футов
3) Чтобы найти длину одной стороны, вам понадобится квадратный корень (√) из 435 600, что равно 660 погонных футов
4) 660 (погонных футов) x 4 (стороны) = 2640 погонных футов для ограждения 10 акров.
Точно так же у многих людей нет даже одного акра. В этом случае вы можете взять долю акра, которая у вас есть, и выполнить описанные выше шаги, чтобы найти общий линейный размер в метражах, необходимый для ограждения вашей собственности.
Пример 3 — Расчет количества забора для ограждения 1/4 акра земли:
1) Один акр = 43 560 квадратных футов
2) 1/4 акра = 0,25 x 43 560 квадратных футов — или — 10 890 квадратных футов
3) Чтобы найти длину одной стороны, вам понадобится квадратный корень (√) из 10 890, который равен 105 погонных футов
4) 104 (погонных футов) x 4 (стороны) = 420 погонных футов, чтобы охватить четверть акра.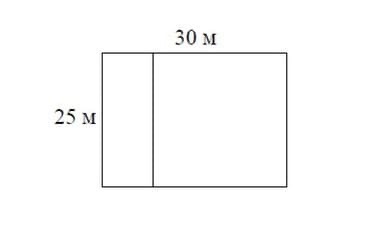
С этой новой найденной информацией легко оценить общую стоимость ограждения для ограждения вашей собственности.Если, например, забор из цепных звеньев высотой 4 фута стоит 4,56 доллара за погонный фут, то приблизительная стоимость одного акра материалов будет составлять 3 812,16 доллара (4,56 доллара на 836 погонных футов), а 10 акров — 12 038,40 доллара (4,56 доллара на 2640 погонных футов). футов), а если вы оцениваете стоимость четверти акра, это будет стоить 1 915,20 долларов в материалах (4,56 долларов на 420 погонных футов).
Пожалуйста, не стесняйтесь использовать калькуляторы ниже, чтобы найти свои ориентировочные затраты и списки материалов, если вы воспользуетесь приведенными выше формулами для определения общего количества необходимых вам ограждений.
Забор вокруг ручки
Привет, Дэрил.
Думаю, я смогу хотя бы ответить на первую часть вашего вопроса.
Вы пытаетесь найти способ максимально увеличить площадь вашего вольера,
поэтому первое, что вам нужно найти, это форму.
Метод, который сразу же приходит на ум, — это метод на вашей диаграмме — прямоугольная ручка. Площадь прямоугольника A = L x W. Периметр прямоугольника прямоугольник 2L + 2W. Если мы используем здание для расширения нашего забора по периметру, тогда общий периметр ограждения может быть 40 + 20 + 100 = 160 линейные ноги.Это означает, что мы можем найти ширину:
160 = 2 л + 2 Вт
становитсяШ = 80 — Д
Используя это, чтобы выразить Площадь A,
На этом этапе вы можете попытаться найти максимум, используя производную этого выражения, чтобы найти нулевой наклон:
Итак, установив эту производную на ноль, L будет равно 40. Это означает, что когда L = 40, площадь вашего прямоугольного пера увеличена до максимума. Поскольку W = 80 — L, то ширина тоже 40.Вот фотография, на которой изображен размер 40 x 40 футов. ограждение (1600 кв. футов) с использованием 100-футового ограждения:
Это простой подход, , но дает ли прямоугольная форма наибольшая площадь?
Не вдаваясь в подробности доказательства, учтите, что если бы у нас было 160 футов ограждения (и без здания), наш самый большой прямоугольник площади будет таким, как показано выше, но если мы нарисуем окружность, окружность которой, C составляет 160 футов, тогда радиус равен
а площадь
квадратный фут! Это значительно больше, чем 1600 кв. футов мы получили, используя прямоугольный (квадратный) подход.
Мы хотели бы использовать эту идею для решения нашей проблемы, но на самом деле у нас нет полного круга.
Тем не менее, мы можем использовать ограждение, чтобы сформировать круговой лепесток, примерно так:
футов мы получили, используя прямоугольный (квадратный) подход.
Мы хотели бы использовать эту идею для решения нашей проблемы, но на самом деле у нас нет полного круга.
Тем не менее, мы можем использовать ограждение, чтобы сформировать круговой лепесток, примерно так:
Мы знаем, что длина дуги составляет 100 футов — вот сколько у нас ограждений. Но при этом Дело в том, что мы не совсем точно определили, какой площади новый корпус. Так давайте перерисуем нашу диаграмму, добавив несколько дополнительных опорных линий, точек и углов, помеченных:
Теперь корпус состоит из трех частей:
Площадь первого треугольника равна половине основания, умноженной на высоту: 1 / 2 x 40 x 20 = 400 кв.футов Вот и готово.
Площадь второго треугольника может быть найдена, если нам известны длины всех сторон. Формула Герона говорит, что его площадь составляет
, где a , b , c — длины сторон
и s — половина периметра ( a + b + c ). В нашем случае мы знаем, что длинная сторона — это гипотенуза первого треугольника, поэтому
используя теорему Пифагора, можно:
В нашем случае мы знаем, что длинная сторона — это гипотенуза первого треугольника, поэтому
используя теорему Пифагора, можно:
Две другие стороны треугольника равны радиусу круга, что мы не пока знаю.
Площадь круглой формы зависит от радиуса и угла наклона, ни то, ни другое мы еще не знаем, но мы знаем длину дуги. Это сумма ограждения: 100 футов. Помните, что если вы работаете в радианах вместо углов, дуга длина — это просто угол, умноженный на радиус. Итак, если широкий угол называется β , тогда 100 = β r или r = 100 / β .
Вернемся ко второму треугольнику. На предыдущей диаграмме мы разделили его дальше. Обратите внимание, что он должен быть равнобедренным, потому что две его стороны одинаковые ( r ). Это означает, что мы можем разделить другую сторону перпендикуляром, проходящим через точка, соединяющая равные стороны. Вот снова этот разделенный треугольник:
Поскольку мы разделили AB пополам, легко увидеть, что треугольник AMC конгруэнтен треугольнику BMC,
поэтому, если мы решаем одно, мы решаем и другое. Давайте внимательно посмотрим на AMC. Мы знаем длину
AM — это половина гипотенузы первого треугольника, h :
Давайте внимательно посмотрим на AMC. Мы знаем длину
AM — это половина гипотенузы первого треугольника, h :
(мы обозначили это z на нашей диаграмме). Линия от M до C перпендикулярна AM, так что это прямой угол в M. Это означает что синус угла Q равен z / r . Мы знаем z , но здесь все еще есть два неизвестных. Давайте решать для r :
Но мы можем быстро заметить, что предыдущий угол β прибавил к двум Q с дает полный круг.Это означает, что β = 2π — 2 Q . Таким образом,
А! Теперь у нас есть два уравнения для r , мы можем решить для Q !
Здесь я собираюсь немного схитрить. Хотя в этом
уравнение, его немного сложно решить точно, и для ограждения приближение будет
делать. ( Боковое примечание: Харли объясняет это в затруднительном положении от Амандипа.
Вот. Если вы попробуете некоторые значения Q, вы можете довольно быстро найти хорошее приближение.
Q = 1,12452 радиана. Теперь, когда мы знаем Q, мы можем найти радиус r : Зная радиус, мы знаем все три длины этого треугольника ABC, поэтому мы
вычислить полупериметр, а затем использовать формулу Герона для вычисления его площади: Кроме того, знание радиуса позволяет нам вычислить β , потому что если r = 100 / β , затем Теперь вооружившись радиусом r и углом β , мы можем
вычислить площадь круглой области, умножив площадь полного круга
отношением β к углу полного круга (в радианах, то есть 2π конечно): Теперь у нас есть все три области. Их сумма: Итак, Дэрил, решать тебе: Для максимально возможного прямоугольного шкафа используйте квадрат размером 40 на 40 футов.
что составляет 1600 кв. футов площади. Однако, если вам нужен корпус наибольшего размера , используйте круглая форма забор и получаем 1879 кв.футов . Стивен Ла Рок> Привет Дэрил, Странная формулировка второй проблемы. Я думаю, вы хотите свести к минимуму материал забора, чтобы минимизировать стоимость. Я также предполагаю, что вам нужна прямоугольная ручка. Если это так, то площадь пера составляет 1800 квадратных футов и, следовательно, Д Ш = 1800 Длина ограждения, которую я назову F, равна F = 2L + 2W — 60 Используйте приведенную выше формулу площади, чтобы записать F как функцию одной переменной, а затем используйте исчисление, как это сделала Сью, чтобы минимизировать количество материала ограждения. Пенни Используйте это руководство, чтобы определить, сколько проволоки вам нужно для ограждения двора. Эти цифры являются приблизительными и основаны на типовых схемах. Вам может понадобиться больше проволоки, если вы делаете внутренние петли для ограждения садов, бассейнов или других охраняемых территорий. Мы предоставим вам проволоку с шагом 500 футов на катушках по 500 футов. Для больших площадей используйте следующую формулу: Умножьте общую площадь на 43 560- i. Найдите квадратный корень из вышеуказанного числа — квадратный корень из 435 600 = 660 (это длина каждой стороны квадратной площади площадью 10 акров. Даже если ваша площадь не квадратная, Если вы умножите это число на четыре, это приблизительная длина четырех сторон площади в 10 акров.) Следовательно, потребуется около 2640 футов проволоки, чтобы оградить периметр площади в 10 акров. Вам понадобится дополнительный провод для подключения передатчика к периметру и / или для любых внутренних петель и т. Д. Важно, чтобы вы правильно спланировали, прежде чем строить забор; вы не хотите, чтобы материалы заканчивались на полпути к установке. Чтобы правильно оценить количество пикетов, необходимых для вашего забора, вы должны определить следующие важные факторы, касающиеся вашего забора: Периметр забора Периметр забора — это общая длина вашего забора. Длина ворот Это следует учитывать только в том случае, если вы будете использовать другие материалы для своих ворот или будете использовать дерево, но вы разместите пикеты иначе, чем расстояние между линиями забора.Если это так, вам нужно иметь отдельную оценку количества пикетов, необходимых на ваших воротах, которое довольно легко оценить, и добавить его к количеству пикетов, необходимых для вашей линии забора. Но не забудьте вычесть ворота из измеренной вами длины забора! Ограждение конфиденциальности или нет Вид забора также существенно влияет на количество необходимых вам пикетов. Для уединения (вместо декоративных) заборов пикеты расположены близко друг к другу, чтобы люди не могли видеть ваш двор через забор. Рядом или внахлест После того, как вы выберете тип ограждения, которое вы будете устанавливать, вам нужно будет решить, хотите ли вы установить их рядом или внахлест. Штакетник с перекрытием требует больше материалов, чем штакетный забор. Оценка пикета частного ограждения Если вы решили установить частный забор, таблица ниже поможет рассчитать необходимое количество пикетов по всему периметру: Таблица множителей пикетов для ограждения конфиденциальности ( на фут периметра ограждения ) Размер пикета Множитель Рядом Перекрытие / Доска на борту 3. 4,4 3 4 2,2 2,9 2 2,45 Чтобы оценить общее количество пикетов забора, используйте эту формулу: [(периметр забора — длина ворот) x множитель] + количество пикетов на ворот Оценка штатного штакетника Таблицы множителей для заборов обычного типа не будет, так как вы решаете, как далеко друг от друга вы будете устанавливать пикеты.Ниже приведена формула, которая поможет вам в этом вычислении: [(Периметр забора — Длина ворот) ÷ (Ширина пикета + расстояние между пикетами)] + количество пикетов на воротах Эти формулы помогут вам оценить количество пикетов, которое вам понадобится для всего вашего забора. ) Мы знаем
что 0
) Мы знаем
что 0 24,788 футов 47.149 футов 239,2 кв. Футов 4.0341 радиан 1239.  4 кв. Футов
4 кв. Футов 1879 кв. Футов 
Калькулятор проволоки для заборов для домашних животных
Для покрытия этой площади Вам нужно это количество провода 1/3 акра 500 футов 1/2 акра 600 футов 1 акр 1000 футов 2 сотки 1300 футов 3 сотки 1500 футов 4 сотки 1800 футов 5 соток 2000 футов  е. 10 акров x 43 560 = 435 600
е. 10 акров x 43 560 = 435 600 Формулы оценки пикета
 Если область, которую вам нужно заключить, представляет собой прямоугольник, периметр — это общая длина всех четырех сторон. Чтобы получить это измерение, все, что вам нужно сделать, это измерить вдоль линий забора, пока не дойдете до того места, откуда начали. Запишите эту информацию для дальнейшего использования.
Если область, которую вам нужно заключить, представляет собой прямоугольник, периметр — это общая длина всех четырех сторон. Чтобы получить это измерение, все, что вам нужно сделать, это измерить вдоль линий забора, пока не дойдете до того места, откуда начали. Запишите эту информацию для дальнейшего использования. Для частных ограждений, очевидно, потребуется большее количество пикетов, чем для ограждений других типов. Тип забора, который вы установите, потребует использования различных формул для расчета вашей оценки.
Для частных ограждений, очевидно, потребуется большее количество пикетов, чем для ограждений других типов. Тип забора, который вы установите, потребует использования различных формул для расчета вашей оценки. 1 x 4 (3½ дюйма) 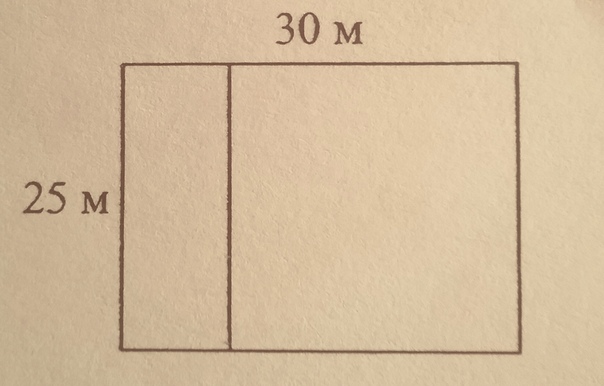 3
3 1 x 4 Полный 4 дюйма 1 x 6 (5½ дюйма) 1 x 6 Полный 6 ” 


 Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.

 Это существенно снижает время прохождения таможни, а значит увеличивает скорость доставки груза!
Это существенно снижает время прохождения таможни, а значит увеличивает скорость доставки груза!
Добавить комментарий